| MODELOVÁNÍ V MECHANICE | OSTRAVA, ÚNOR 2007 |
1 Ing. Petr Frantík, Ph.D., Vysoké učení technické v Brně, Fakulta stavební, Ústav stavební mechaniky, Veveří 331/95, 602 00 Brno, e-mail: frantik.p@fce.vutbr.cz
Abstract
An analysed postcritical behaviour of a long plate is described in this paper. Postcritical state is obtained by axial-torsional buckling of ideal symmetrical slender plate of elastic material. Its poscritical behaviour is fruitful in number of possible states. Also bifurcation diagrams are shown here. Analyses were provided by numerical simulations with special model created by physical discretization.
1 Úvod
Ztráta stability konstrukcí se řadí k nejnáročnějším úlohám jak z hlediska teoretického popisu, tak i při numerickém řešení. Ztráta stability znamená dosažení kritického bodu (často se jedná o tzv. bifurkaci) v němž konstrukce přechází na nový stav prudkým přechodovým jevem, který nazýváme katastrofou, viz Arnold (1983) [1]. Pro výpočet deformací pružných konstrukcí při dosažení ztráty stability si již nevystačíme s lineárním modelem a to i v případě, uvažujeme-li lineární chování materiálu. Zvláště při sledování pokritického působení je třeba užít model, který nezanedbává změny geometrie konstrukce. I s tímto požadavkem může být model co do podstaty jednoduchý a vystihující klíčové aspekty úlohy. Analytická řešitelnost takového modelu je ale zpravidla velmi obtížná, jelikož jeho popis obsahuje silně nelineární členy.
Obtížnost úloh ztrát stability se objevuje i při numerickém řešení. Tradiční metody pro diskretizaci kontinua, z nichž nejpoužívanější je metoda konečných prvků, se ukazují jako neefektivní, jak z hlediska složitosti výpočtu, tak i z hlediska časové náročnosti. Objevuje se zde prostor pro alternativní metody, více zaměřené na typické rysy pokritických úloh. Přehled alternativních metod uvádí studie Henrych (1985) [2]. Důležitou roli hraje změna přístupu k analýze těchto úloh ve smyslu nelineárních dynamických systémů, viz např. Macur (1995) [3]. Cílem je nalézt model, jehož chování se bude kvalitativně shodovat s modelovanou úlohou. Kvantitativní kritéria shody zde nejsou tak podstatná.
Jak je dále uvedeno, vybraná úloha vykazuje typické rysy silně nelineárního systému. Dochází ke katastrofám, objevují se bifurkační body, existuje zde současně více než jeden výsledný statický stav.
2 Úloha
Přímý prut konstantního průřezu zatížený osovým tlakem může ztratit stabilitu díky vybočení kroucením (angl. axial-torsional buckling, viz např. Bažant a Cedolin 1991 [4]). Pro úplnost poznamenejme, že v článku (Frantík 2006) [5] byla modelována ztráta stability kroucením u jednoose symetrického L-profilu. Zde se pozornost věnuje prutu ve tvaru tenkého pásu – desce o rozměru 1.0 krát 0.2 metru, viz obr. 1. Příčinou vybočení desky kroucením může být její nízká kroutící tuhost, nebo zabezpečení proti vybočení ohybem (střednice deskového prutu zůstává přímá).

Obr. 1: Centricky tlačený deskový prut
Deskový prut je uvažován o hmotnosti m = 1 kg z lineárního materiálu s normálovou tuhostí EA = 1 MN.m-1, smykovou tuhostí v rovině desky GAk = 0.1 MN.m-1, ohybovou tuhostí ve směru kolmém na rovinu desky EI = 100 Nm.rad-1 a tuhostí v kroucení okolo střednice GIt = 10 Nm.rad-1.
3 Model
Model deskového prutu je založen na fyzikální diskretizaci. Fyzikální diskretizací myslíme nahrazení spojitého pružného kontinua soustavou pružin (nehmotných, popř. obecněji hmotných) spojujících hmotné body (obecněji hmotné tuhé elementy), jejichž stav lze popsat diskrétní množinou stavových proměnných. Předpokládáme, že chování takového modelu vystihuje podstatné rysy úlohy při nižších nárocích na výpočetní i časovou složitost.
Na obr. 2 je znázorněno rozdělení deskového prutu na obdélníkové dílce, v jejichž vrcholech jsou umístěny hmotné body. Zatížení osovým tlakem je provedeno pomocí rovnoměrně rozložených sil, působících ve směru střednice nezdeformovaného prutu, na jeho volných koncích, viz obr. 2. Centrální hmotné body se mohou pohybovat pouze ve směru střednice deskového prutu. Ačkoliv tato okrajová podmínka není postačující k zajištění statické určitosti úlohy, není vhodné další podmínku přidávat z důvodu symetrie dynamických jevů.
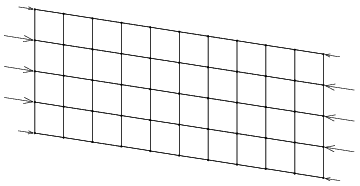
Obr. 2: Model deskového prutu
Každý obdélníkový dílec, ze kterého se model prutu skládá, obsahuje vnitřní pružiny, jejichž schémata jsou zobrazena na obr. 3. Jedná se o liniové pružiny zajišťující normálovou tuhost a přenos ohybových momentů mezi hmotnými body (viz dále), smykové pružiny pro přenos smyku v rovině dílce a torzní pružiny pro zajištění kroutící tuhosti dílce.

Obr. 3: Schémata vnitřních pružin dílce
Již bylo zmíněno, že liniové pružiny plní rovněž funkci přenosu ohybových momentů. Proto jsou znázorněny na obr. 3 jako teleskopické tyče. Množinu pružin je totiž třeba doplnit rotační pružinou zajišťující vzájemnou ohybovou tuhost dvou spojených dílců. Znázornění této pružiny a její napojení na teleskopické tyče je vidět na obr. 4.
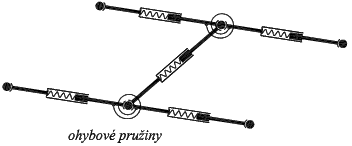
Obr. 4: Schéma rotační pružiny pro přenos ohybu
Všechny typy popsaných pružin jsou v modelu uvažovány jako lineární, přičemž je pro definici jejich napjatosti užit úplný geometrický popis, viz publikace Frantík (2006) [6]. Množina popsaných pružin zřejmě vytváří model prutu reflektující všechny podstatné přetvárné vlastnosti.
Model je uvažován jako disipativní dynamický systém s polynomiálním viskózním útlumem, viz (Frantík 2006) [6], řešený numericky klasickou metodou Runge-Kutta. Úloha je tedy formulována dynamicky s tím, že statický stav je obdržen po ustálení systému do klidového stavu.
4 Simulace
Deskový prut byl pro účely numerické simulace rozdělen na 8 krát 20 dílců (vyšší počet dílců je po délce deskového prutu). Jedinným proměnlivým a zároveň řídícím parametrem je velikost výslednice osových sil F, díky které je prut osově tlačen. Získání různých stavů pro stejnou hodnotu síly F lze ovlivnit počátečními podmínkami úlohy nebo způsobem nanášení zatížení.
Provádění simulací mělo za cíl zjistit, jakých pokritických statických stavů je po ztrátě stability dosahováno, a jak tyto stavy přecházejí jeden do druhého při změně zatěžující síly F.
4.1 Pokritické stavy
Možné pokritické stavy byly hledány následujícím způsobem: Model prutu je v počátečním okamžiku umístěn do prostoru s nulovou rychlostí, prakticky nenapjatý, zatížený plnou silou F. Právě jeden jeho rohový hmotný bod je umístěn mimo rovnovážnou polohu v nenapjatém stavu. Tato počáteční poloha se odlišuje od rovnovážné pouze o hodnotu řádově 10-13krát menší než je délka prutu. Účelem této podmínky je zavedení velmi malé dynamické nesymetrie. Jinak totiž model nevybočí (tento fakt je svázán s umístěním a orientací deskového prutu v konkrétním souřadném systému v počítači). Simulace probíhá tak dlouho, dokud není nalezen statický stav.
Nalezené stavy lze rozdělit do dvou kategorií: na symetrické a nesymetrické. V každé kategorii se stavy dále odlišují podle počtu vln, které se po vybočení vytvoří. Stavy byly hledány v rozsahu síly F = 3 až 14 kN. Přehled je vidět na obr. 5, jejich výskyt v tab. 1.
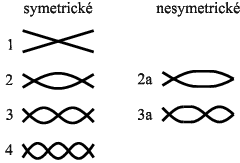
Obr. 5: Rozdělení pokritických tvarů
Z tabulky 1 je patrné, že index dosaženého tvaru stoupá s velikostí síly F. Nicméně např. pro sílu F = 13 kN se prut ustálil do tvaru s indexem 1. V tomto smyslu bude zřejmě obtížné popř. nemožné předvídat do jakého tvaru se systém za daných podmínek ustálí.

Tab. 1: Dosažené pokritické tvary pro různou sílu F
Pro upřesnění uveďme, že schémata tvarů na obr. 5 jsou přibližná v tom smyslu, že při zvětšování síly F budou vypadat v průmětu jinak. Doplňme, že tvary s více vlnami nejsou spirálovitě zatočené, jak se z průmětu zdá. Pro lepší představu je na obr. 6 zobrazen symetrický tvar s indexem 4 dosažený při síle F = 10 kN.
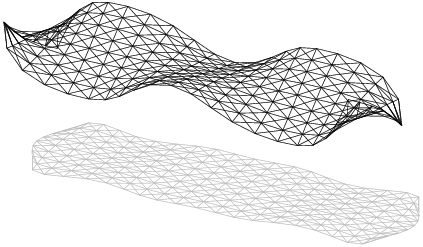
Obr. 6: Symetrický tvar s indexem 4 při síle F = 10 kN (včetně půdorysu)
Symetrické tvary s lichým indexem mají proměnné vzájemné pootočení koncových průřezů deskového prutu okolo střednice, typicky nenulové. Sudé symetrické tvary se naopak vyznačují nulovým vzájemným pootočením koncových průřezů, viz obr. 6.
U prvních dvou symetrických tvarů byla pomocí simulace měřena kritická síla. První symetrický tvar má kritickou sílu Fcr1 = 597 N. Druhému symetrickému tvaru odpovídá kritická síla Fcr2 = 789 N.
Speciální pozornost si zasluhují oba nesymetrické tvary. V simulaci vznikají ztrátou symetrie úlohy z vyšších symetrických tvarů. Nesymetrický tvar 2a (viz obr. 7) vzniká ze symetrického tvaru s indexem 4. Nesymetrický tvar 3a (viz obr. 8) zřejmě vzniká ze symetrického tvaru s indexem 5.
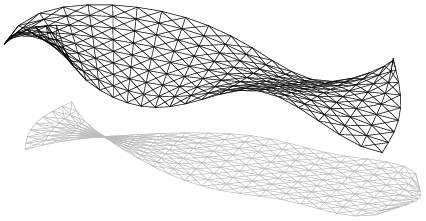
Obr. 7: Nesymetrický tvar s indexem 2a při síle F = 8 kN
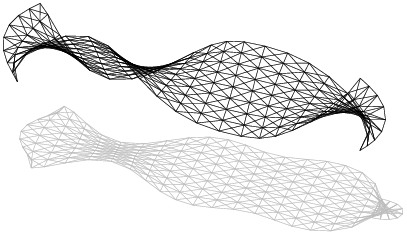
Obr. 8: Nesymetrický tvar s indexem 3a při síle F = 14 kN
4.2 Bifurkační diagramy
Pro zjištění návaznosti jednotlivých pokritických stavů byly provedeny simulace, při kterých se zatěžovací síla F plynule měnila. Na počátku byla nastavena síla F na určitou hodnotu, která se v čase lineárně snižovala k nule. Doba simulace byla pokaždé nastavena na 3 sekundy. Jako stavová proměnná pro vynášení bifurkačních diagramů bylo vzato pootočení koncových průřezů prutu.
Výsledkem simulací je zjištění, že jednotlivé liché tvary při ztrátě stability preferují přechod na nižší liché tvary a sudé naopak. Zmapované přechody jsou znázorněny na obr. 9. Příslušné bifurkační diagramy je možno vidět na obr. 10 a 11.
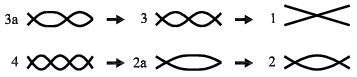
Obr. 9: Přechody mezi pokritickými tvary při snižování síly F
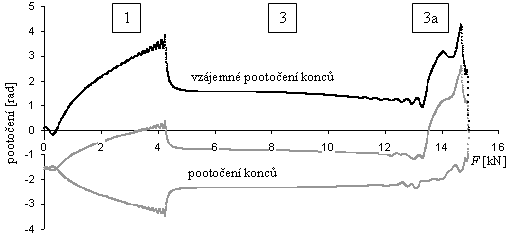
Obr. 10: Bifurkační diagram přechodů 3a-3-1 (snižování síly F z hodnoty 15 kN)
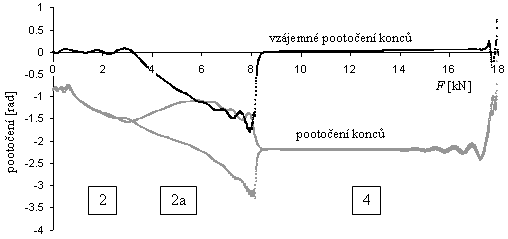
Obr. 11: Bifurkační diagram přechodů 4-2a-2 (snižování síly F z hodnoty 18 kN)
Z důvodu časové náročnosti jsou bifurkační diagramy nepřesné díky dokmitávání prutu při náhlých změnách stavu. I přesto v nich lze snadno rozpoznat bifurkační body a náhlé katastrofické přechody mezi pokritickými tvary.
Simulace v případě digramu na obr. 10 probíhala následovně: Prut po zatížení silou F = 15 kN náhle vybočil a ustálil se do nesymetrického tvaru 3a. Po snížení síly F pod hodnotu asi 13.7 kN nastal pád na symetrický tvar 3, který byl stabilní až do hodnoty cca 4.8 kN. Poté došlo k přechodu na symetrický tvar 1. Přechod mezi symetrickými tvary probíhá jako zánik jedné vlny. Nakonec došlo k překročení bifurkačního bodu Fcr1 = 597 N, při kterém se prut ustálí do přímého tvaru (prekritický stav).
Simulace dokumentovaná digramem na obr. 11 měla následující průběh: Prut po zatížení silou F = 18 kN se po vybočení ustálil se do symetrického tvaru 4. Po snížení síly F pod hodnotu asi 8.4 kN nastal pád na nesymetrický tvar 2a, který byl stabilní až do hodnoty cca 3.4 kN. Poté došlo k přechodu na symetrický tvar 2, který zůstal stabilní do dosažení bifurkačního bodu Fcr2 = 789 N. Překročení bifurkačního bodu mohlo vést k vybočení do symetrického tvaru 1, ovšem k této události nebyl dostatek času vzhledem k dokmitávání prutu a relativně rychlému snižování zatěžující síly.
5 Závěr
V článku byly prezentovány výsledky numerických simulací pokritického působení prutu ve tvaru štíhlé desky zatíženého osovou tlakovou silou, který vybočuje kroucením. Prut byl reprezentován pomocí speciálního modelu vzniklého fyzikální diskretizací.
Úloha se ukázala jako velmi bohatá na možné pokritické stavy. Nalezené stavy byly rozděleny do dvou kategorií na symetrické a nesymetrické. Analyzovaly se rovněž přechody mezi těmito stavy, které probíhaly jak katastrofickým způsobem, tak zánikem v bifurkačním bodu.
Charakteristická vlastnost této úlohy je obtížná identifikace pokritického tvaru, zejména s ohledem na možné nesymetrické tvary a jejich vznik/zánik. Poznamenejme, že díky bohatosti, lze očekávat zajímavé rozložení plochy potenciální energie systému.
Poděkování
Tento výsledek byl získán za finančního přispění MŠMT, projekt 1M6840770001, v rámci činnosti výzkumného centra CIDEAS. Při řešení byly částečně využity teoretické výsledky dosažené v projektu GAČR 103/07/0760.
Literatura
[1] Arnold, V., I., TEÓRIA KATASTROF (orig. TEORIJA KATASTROF, vydavatelstvo Moskevské univerzity 1983), vydavateľstvo Alfa, Bratislava, 1983
[2] Henrych, J., ÚPLNÁ SOUSTAVA FINITNÍCH METOD MECHANIKY A MOŽNOSTI DALŠÍHO ROZVOJE, studie ČSAV 6.85, nakladatelství Akademia, Praha, 1985
[3] Macur, J., ÚVOD DO TEORIE DYNAMICKÝCH SYSTÉMŮ A JEJICH SIMULACE, skripta, nakladatelství PC-DIR, Brno, 1995
[4] Bažant, Z., P., Cedolin, L., STABILITY OF STRUCTURES, Oxford University Press, Oxford, 1991
[5] Frantík, P., MODELOVÁNÍ ZTRÁTY STABILITY PRUTU KROUCENÍM PŘI OSOVÉM TLAKU, sborník příspěvků Setkání kateder stavební mechaniky, STM FAST VUT v Brně, 2006
[6] Frantík, P., SIMULACE ZTRÁTY STABILITY ŠTÍHLÉHO PRUTU PŘI KROUCENÍ, CD sborník mezinárodní konference Modelování v mechanice, VŠB-TU Ostrava, 2006