CREATION OF THE STABLE ELASTIC LOOP

P. Frantík¹

¹Ing. Petr Frantík, Ph.D., Ústav stavební mechaniky, Fakulta stavební, Vysoké učení technické v Brně, Veveří 331/95, 602 00 Brno, e-mail: kitnarf at centrum dot cz

1. Úvod

Modelování pružných konstrukcí je oborem, jehož aplikace vykazují výbornou shodu s experimenty i za náročných podmínek, jakými jsou velká posunutí. Je-li reálná konstrukce dostatečně štíhlá, pak může dosahovat velmi velkých deformací, při zachování pružného působení materiálu (malá přetvoření). Protože matematický popis konstrukce podrobené velkým deformacím vyžaduje užití nelineárních vztahů, jsou tyto úlohy spolu s předpokladem pružného působení výborným prostředkem ke studiu nelineárních jevů. Tyto výhody jsou všeobecně známé a často využívané. Stačí vzpomenout úlohu vzpěru prutu vyřešenou Leonhardem Eulerem již v roce 1744, která je dodnes studována a předkládána jako názorný příklad tzv. měkké ztráty stability při rozdvojení rovnovážného
stavu - dosažení bifurkačního bodu.

Způsobů, jakým může pružná konstrukce ztrácet stabilitu je více, ovšem je dokázáno, že jejich počet je omezený. Nejlepší vhled do této problematiky nabízí v současnosti zřejmě teorie katastrof, která studuje singularity hladkých zobrazení, viz [Arnold 1983]. Ukazuje se, že na analýzu stability konstrukcí lze nahlížet jako na hledání singularit hladkých zobrazení.

Výzkum doprovázející vznik teorie katastrof ukázal, že studované systémy lze rozdělit do dvou skupin na tzv. typické, které nejsou citlivé na malou změnu svých parametrů a na systémy netypické, jejichž malá změna způsobí, že se z nich stanou systémy typické. Netypické systémy, jako je např. vzpěr dokonale symetrického prutu, se reálně nevyskytují a nazývají se rovněž degenerované. Jejich přechod na systém typický je často doprovázen ztrátou symetrie, jako je tomu právě při vzpěru prutu. Již Henri Poincaré poukázal, že při studiu systémů s proměnlivými parametry se nelze vyhnout degenerovaným systémům, jelikož tyto rozdělují oblasti parametrů odpovídajících systémům typickým (též regulárním).

Tento příspěvek se věnuje modelování dokonale symetrického pružného prutu (tj. netypického systému), zatíženého dvojicí kroutících momentů. Účelem je modelovat ztrátu stability při kroucení a získat tak pokritický stabilní stav prutu ve tvaru smyčky. Smyčka vzniká i u jednodušších systémů jako je vzpěr prutu, viz obr. 1, nebo ohyb konzolového nosníku, ovšem jak bylo ukázáno v příspěvcích [Frantík 2002, Frantík2004], vznikem smyčky se statický stav stává nestabilním. Jedná se o případ tzv. tvrdé, popř. také katastrofické ztráty stability.

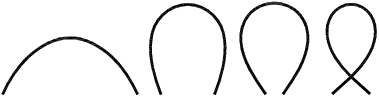
Obrázek 1: Vznik smyčky při pokritickém vzpěru přímého prutu

Po prokázání nestability takto vzniklé smyčky se nabízela otázka, zdali existuje podobný systém, při kterém vzniká smyčka stabilní. Inspirací při hledání takového systému byl jev, ke kterému dochází při kroucení štíhlého \uv{prutu} jakým je např. vlákno letecké gumy. Lze snadno vyzkoušet, že při kroucení vlákna, potažmo velmi štíhlého prutu, vzniká v určitém okamžiku smyčka, která se jeví jako stabilní.

2. Kroucení štíhlého prutu

Mějme prizmatický prut zatížený na svých koncích proti sobě působícími, stejně velkými kroutícími momenty, viz obr. 2. Při nárůstu velikosti kroutících momentů M nad určitou kritickou hodnotu M_cr dochází ke ztrátě stability přímého tvaru prutu, prut se zakřivuje a střednice prutu se stává prostorovou křivkou (přehled viz [Bažant & Cedolin 1991]).

Obrázek 2: Schéma kroucení přímého prutu

Pro dynamickou simulaci této úlohy byl vytvořen model pomocí fyzikální diskretizace. Fyzikální diskretizací je myšleno nahrazení spojitého prutu soustavou pružin a tuhých dílců. Taková soustava pak je popsána diskrétní množinou stavových proměnných, čímž je umožněno efektivně řešit daný problém. Přehled a zařazení modelu do výpočetních metod mechaniky lze nalézt v [Henrych 1985].

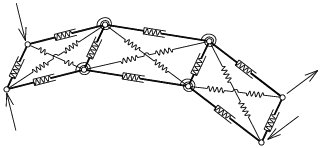
Prut je po délce rozdělen na obdélníkové dílce s vnitřními pružinami, nahrazujícími normálové a smykové přetvoření. Dílce jsou vzájemně spojeny klouby s rotačními pružinami nahrazujícími "ohybové" přetvoření, viz obr. 3.

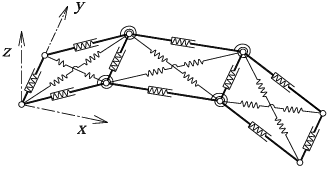
Obrázek 3: Schéma modelu prutu

Oba druhy pružin jsou lineární. Normálové a smykové pružiny působí silou přímo úměrnou prodloužení pružiny, rotační pružiny působí momentem přímo úměrným vzájemnému natočení dílců v místě připojení (kloub). Tyto závislosti můžeme popsat vztahy:

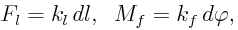(1)

kde F_l je síla, kterou liniová pružina (normálová resp. smyková) působí na přípojné klouby, k_l je tuhost liniové pružiny, dl je protažení liniové pružiny; M_f je moment, kterým rotační pružina působí na připojené dílce, k_f je tuhost rotační pružiny a d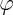 je natočení dílců v místě připojení pružiny. Pro přetvoření liniové pružiny dl_ij spojující klouby i a j lze užít geometricky přesného popisu:

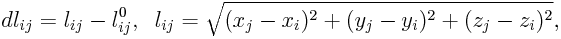(2)

kde x_i, y_i, z_i jsou aktuální souřadnice kloubů, l_ij je aktuální délka pružiny, původní délka nenapjaté pružiny je l⁰_ij. Podobně pro přetvoření rotační pružiny d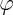_ijk ležící na kloubu j a vázané na klouby i a k (viz obr. 3) lze psát geometricky přesně:

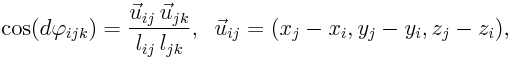(3)

kde 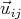je pomocný vektor daný polohou kloubů i a j.

Předpokládejme, že hmotnost prutu lze soustředit do kloubů na hranách prutu. Za tohoto předpokladu vzniká n hmotných kloubů, na které působí připojené pružiny výslednou interakční silou 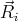složenou z účinků pružin daných vztahy (1). Potom lze psát pohybové rovnice ve tvaru:

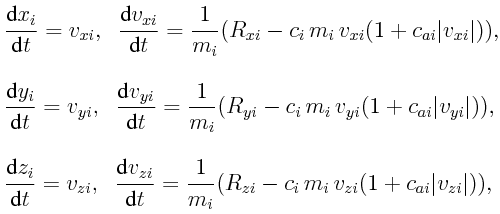(4)

kde v_xi, v_yi, v_zi jsou složky aktuální rychlosti i-tého hmotného kloubu, R_xi, R_yi, R_zi jsou složky aktuální interakční síly 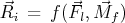působící na hmotný kloub i, m_i je hmotnost i-tého hmotného kloubu, c_i je součinitel útlumu, c_ai je součinitel kvadratického člene útlumu a t je čas. Dodejme, že popsaný model je nelineární, viz vztahy (2) a (3), a téměř nezávislý na velikosti posunutí hmotných kloubů.

Řešení pohybových rovnic je vzhledem k silné nelinearitě systému prováděno klasickou numerickou metodou Runge-Kutta.

 ;

Zatížení kroutícími momenty

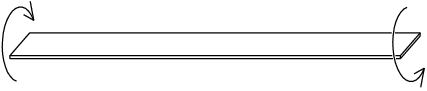
Vzhledem ke zvolené diskretizaci úlohy je zřejmé, že nanesení kroutících momentů je třeba provést pomocí dvojic sil (tj. sil stejně velkých, opačného směru). Uvažování velkých posuvů bodů prutu pak vede k problému se zachováním podmínky dvojice sil i jejího momentového účinku, viz obr. 4.

Obrázek 4: Zatížení kroutícími momenty

Pro zachování momentového účinku dvojice sil při velkých rotacích konců prutu byl zvolen přístup tzv. sledujícího zatížení, kdy každá síla mění svůj směr v závislosti na natočení modelu prutu v místě působiště sil (jedná se o tzv. nekonzervativní zatížení). Zachování podmínky dvojice sil je udržováno stanovením společného natočení pro obě síly z dvojice. Užití sledujícího zatížení má na úlohu určité negativní účinky, které budou ukázány dále.

 ;

3. Simulace

Model prutu je dokonale symetrický. Jediná nesymetrie, objevující se při reprezentaci modelu v počítači, bude dána polohou prutu v souřadném systému a nesymetrií danou zaokrouhlovací chybou, kterými je stav modelu popsán. Nesymetrie digitalizovaného modelu je natolik malá, že malé "pohybové" nesymetrie v počátečních podmínkách (rozložení rychlostí hmotných kloubů) mohou mít převažující vliv. Směr vybočení prutu tak může probíhat typicky nepředvídatelně. Význam zavedení nesymetrických počátečních podmínek lze spatřovat kromě výše uvedeného rovněž ve zkrácení času, kterého je pro vybočení modelu prutu zapotřebí.

Prozatím jsme se nezmínili o okrajových podmínkách prutu. Jejich vliv na chování prutu je značný, a proto se zde soustředíme jen na zcela volný prut.

Při ztrátě symetrie prutu, v důsledku užití sledujícího zatížení, může dojít k rotaci modelu prutu jako celku, jelikož dvojice kroutících momentů přestane mít nulovou výslednici. Z tohoto důvodu nebude zcela zřejmá případná stabilita získané smyčky ve smyslu stability statického stavu. Za stabilní stav proto obecněji považujme pohybující se prut, který nemění svůj tvar.

Simulace jsou prováděny následujícím způsobem: Jako počáteční stav je zvolen nepřetvořený model prutu s malou "pohybovou" nesymetrií v počátečních podmínkách. Dvojice kroutících momentů je nanesena v plné velikosti a v průběhu simulace nemění velikost. Parametry modelu prutu jsou zvoleny tak, aby odpovídaly tenkému pásku oceli s převažující délkou (obr. 2). Kromě velikosti kroutících momentů je rovněž uvažována proměnlivost parametrů tlumení. Výsledkem simulace systému pak mohou být následující stavy:

Poznamenejme, že v případě posledních dvou stavů (zejména u prvního z nich) existují dvě důležité možnosti: model prutu při simulaci, resp. při "ustáleném pohybu", změní svůj tvar natolik, že se jeho části protnou či nikoliv. Možnost pronikání částí prutu je pochopitelně v rozporu s realitou.

Obrázek 5: Statický přímý tvar prutu

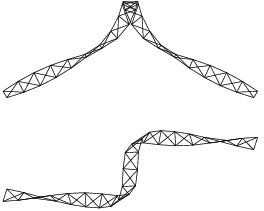
Obrázek 6: Rotující vybočený prut s ustáleným tvarem (dva vzájemně kolmé průměty)

Důležitou roli zde hraje tlumení. Výsledkem ztráty stability je rotace, při které mají hmotné body na konci prutu velkou obvodovou rychlost. Je-li kvadratický člen útlumu výrazný, viz rovnice (4), pak mají konce prutu tendenci se přimknout k ose rotace, k čemuž při užití lineárního útlumu nedochází.

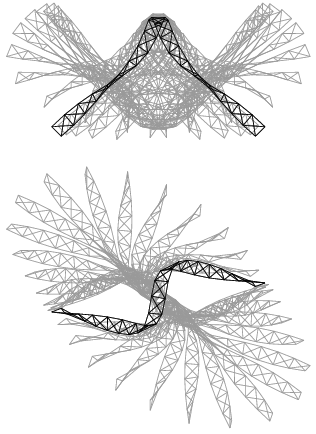
Obrázek 7: Kinogram poloviny periody oscilujícího prutu (dva vzájemně kolmé průměty)

4. Závěr

V příspěvku byla prezentována simulace kroucení dokonale symetrického prutu, umístěného volně v prostoru. Pro reprezentaci prutu bylo užito silně nelineárního modelu, vzniklého fyzikální diskretizací. Vnější kroutící momenty se uvažovaly jako sledující (nekonzervativní) zatížení. Simulace ukázaly, že je takto vzniklý systém bohatý na různé druhy ustálených stavů: Lze dosáhnout klidu, periodického i chaotického pohybu. Kvalitativně různé druhy pohybu bude možné odlišit například sledováním hodnoty vzepětí prutu.

Původní cíl - vznik stabilní smyčky - lze považovat za částečně splněný. K tomu, aby byla smyčka stabilním statickým stavem bude postačovat užití vhodných okrajových podmínek, aby se zamezilo rotaci prutu vzniklé kvůli ztrátě souososti kroutících momentů po vybočení prutu.

Výsledek simulace je obecně značně ovlivněn nemožností kontaktu mezi částmi prutu. Snadno se lze přesvědčit experimentem, např. s leteckou gumou, že "zavinutí" smyčky má na systém stabilizující efekt.

Nekonzervativní zatížení je poměrně náročným prvkem úlohy, jak je patrné např. z publikace [Elishakoff 2005], která přináší rozsáhlý kritický přehled této problematiky. Poznamenejme pouze, že zde bylo užito sledujícího zatížení zejména z důvodu snadnosti jeho definice a nanesení na volný prut. Vhodné okrajové podmínky umožní použití "realističtějšího" konzervativního zatížení.

Zvláštní roli hraje v simulaci tlumení. Ukazuje se, že při rotaci prutu je značný rozdíl mezi útlumem lineárním a nelineárním (nelineární útlum odpovídá např. zvýšenému odporu vzduchu). Nelineární útlum způsobil přimknutí konců prutu k ose rotace.

5. Poděkování

Tento výsledek byl získán za finančního přispění MŠMT, projekt 1M6840770001, v rámci činnosti výzkumného centra CIDEAS. Při řešení byly částečně využity teoretické výsledky dosažené v projektu GA ČR 103/03/1350.

6. Literatura

[Arnold 1983] Arnold, V. I., 1983: Teória katastrof (orig. Teorija katastrof, vydavatelstvo Moskevské univerzity 1983), vydavateľstvo Alfa, Bratislava

[Bažant & Cedolin 1991] Bažant Z. P., Cedolin L., 1991: Stability of Structures, Elastic, Inelastic, Fracture, and Damage Theories, Oxford University Press, New York

[Elishakoff 2005] Elishakoff I., 2005: Controversy Associated With the So-Called "Follower Forces", Applied Mechanics Rewiev, vol. 58, p. 117-142

[Frantík 2002] Frantík, P., 2002: Nestability vybraných systémů, CD sborník konference Inženýrská mechanika 2002, Svratka

[Frantík 2004] Frantík, P., 2004: Stability study of the elastic loop, 5th International PhD Symposium in Civil Engineering, vol. 2, p. 1083-1088, Delft, Netherlands

[Henrych 1985] Henrych, J., 1985: Úplná soustava finitních metod mechaniky a možnosti dalšího rozvoje, studie ČSAV 6.85, nakladatelství Akademia, Praha