| MODELOVÁNÍ V MECHANICE | OSTRAVA, ÚNOR 2006 |
1Ing. Petr Frantík, Ph.D., Vysoké učení technické v Brně, Fakulta stavební, Ústav stavební mechaniky, Veveří 331/95, 602 00 Brno, Česká republika, e-mail: kitnarf at centrum dot cz
Abstract
Paper deals with the stability loss of straight shape of slender ideal prismatic beam under torsion. A special discrete nonlinear numerical model was used for dynamical simulation of the loaded beam. Usage of this model shows, that this stability loss is the supercritical pitchfork bifurcation in terms of the catastrophe theory.
1 ÚVOD
Při modelování mechanických soustav se již tradičně setkáváme se dvěma částečně protichůdnými přístupy. Prvním přístupem lze nazvat vytváření detailních modelů, druhý přístup klade do popředí tzv. minimální model.
Zvyšování úrovně detailu modelu je typické pro úlohy, které jsou svojí podstatou předvídatelné a relativně snadno řešitelné. Vystižení podrobností je také často důležité pro praktické účely, kdy potřebujeme spolehlivě obhájit funkčnost modelu, například když není k dispozici ověřovací experiment.
Oproti tomu modely s minimálním počtem neznámých veličin (stupňů volnosti) lze nalézt zejména tam, kde převažuje problém výpočetní náročnosti. Minimalizujeme-li počet stupňů volnosti, pak musíme zajistit/ověřit, aby model vykazoval ty jevy, které jsou pro jeho funkčnost významné. Uplatnění takového přístupu lze kromě výpočetní rychlosti spatřovat především v teoretické rovině. Takový model, pokud se jej podaří najít, nám může přinést informaci o podstatě modelovaného jevu. Za zmínku rovněž stojí získání zkušeností při vytváření a kontrole takového modelu. Jev samotný pak může být přístupnější k nalezení způsobu, jak ho využít nebo jak se mu vyhnout.
2 Kroucení ideálního prutu
Z hlediska hledání minimálního modelu jsou teoreticky zajímavé zejména ty úlohy, při kterých dochází ke skokové ztrátě stability (tzv. katastrofa, viz [1]). Všeobecně známou je například úloha vzpěru přímého prutu, kterou vyřešil Leonhard Euler již v roce 1744. Podobným problémem je ztráta stability při kroucení přímého štíhlého prutu.
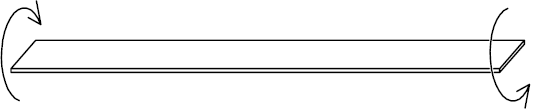
Obr. 1: Kroucení volného prutu
Mějme ideální prut bez vnějších vazeb z dokonale pružného materiálu. Prut zatížíme na jeho volných koncích dvojicí opačných kroutících momentů, jejichž osa je shodná s osou prutu, viz obr. 1. Budeme-li zvyšovat velikost kroutícího momentu (označme jej M), pak v určitý okamžik přestane být přímý tvar zkrouceného prutu stabilním stavem a dojde k náhlému příčnému vybočení. Odpovídající hodnota kroutícího momentu je tzv. kritická s označením Mcr.
Model, který je zde popsán, slouží k prvotnímu přiblížení k podstatě tohoto jevu.
3 Model prutu
Předpokládejme velmi štíhlý prut s průřezem, který je v kroucení poddajný, schopný velkých posunutí, aniž by docházelo k nepružnému přetvoření. Těmto předpokladům vyhovuje například tenký dlouhý plátek z pružné oceli. Model vytvoříme tak, že prut po délce rozdělíme na obdélníkové dílce s vnitřními pružinami, nahrazujícími normálové a smykové přetvoření. Dílce vzájemně spojíme klouby s rotačními pružinami nahrazujícími „ohybové“ přetvoření, viz obr. 2.
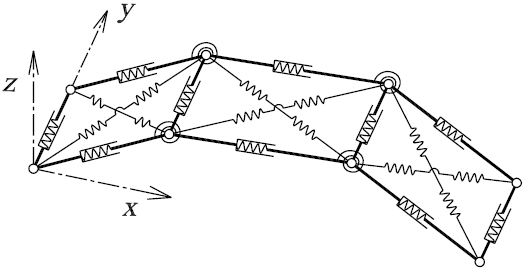
Obr. 2: Model prutu v obecném tvaru (detail dělení na tři dílce)
Působení obou druhů pružin nechť lineárně závisí na velikosti jejich přetvoření. Normálové a smykové pružiny působí silou přímo úměrnou prodloužení pružiny, rotační pružiny působí momentem přímo úměrným vzájemnému natočení dílců v místě připojení (kloub). Tyto závislosti můžeme popsat vztahy:
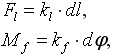| (1) |
kde Fl je síla, kterou liniová pružina (normálová resp. smyková) působí na přípojné klouby, kl je tuhost liniové pružiny, dl je protažení liniové pružiny; Mf je moment, kterým rotační pružina působí na připojené dílce, kf je tuhost rotační pružiny a d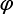
je natočení dílců v místě připojení pružiny. Pro přetvoření pružin lze užít geometricky přesného popisu:
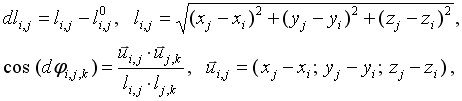 | (2) |
kde xi, yi, zi jsou aktuální souřadnice kloubů, li,j je aktuální délka pružiny spojující klouby s indexy i a j, původní délka nenapjaté pružiny je l0i,j a ui,j je pomocný vektor daný polohou kloubů i,j.
Použitý způsob diskretizace kontinua se nazývá fyzikální diskretizací, viz [2]. Takové nahrazení spojité úlohy lze často s výhodou využít při hledání minimálního modelu. Ukazuje se, že může být, vzhledem k výpočetní složitosti, velmi efektivní, viz [3].
Pro hledání statických stavů prutu zatíženého kroutícími momenty lze využít buď statické nebo dynamické formulace problému. V případě statické formulace sice šetříme výpočetní čas, ale objevuje se nejistota ve vlastnostech nalezeného řešení. Řešení totiž může být stabilní i nestabilní. Navíc může být nalezené řešení nesprávné ve smyslu průběhu zatěžovacího procesu (stav reálně nebude dosažen). Takové případy mohou nastat, existuje-li více stabilních statických stavů.
Z výše popsaných důvodů bylo užito formulace dynamické. Ta je sice výpočetně náročnější, ovšem na správnost dosažení statického stavu a jeho stabilitu se můžeme více spolehnout. Předpokládejme, že hmotnost prutu lze soustředit do kloubů na hranách prutu. Za tohoto předpokladu vzniká n hmotných kloubů, na které působí připojené pružiny dle vztahů (1). Potom lze psát pohybové rovnice ve tvaru:
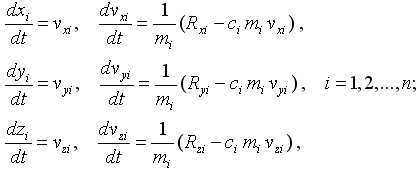 | (3) |
kde vxi, vyi, vzi jsou složky aktuální rychlosti i-tého hmotného kloubu, Rxi, Ryi, Rzi jsou složky aktuální interakční síly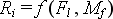 
působící na hmotný kloub i, mi je hmotnost i-tého hmotného kloubu, ci je součinitel útlumu i-tého hmotného kloubu a t je čas.
Dodejme, že popsaný model je nelineární, viz vztahy (1) a (2), a téměř nezávislý na velikosti posunutí hmotných kloubů. Jediné omezení je dáno vztahem pro výpočet pootočení d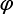, viz (2). Ze vztahu vyplývá 
.
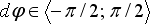4 Simulace
Řešení pohybových rovnic je pro účely simulace prováděno diferenční klasickou Runge-Kuttovou metodou, která je pro řešení nekonzervativního systému tohoto druhu plně postačující.
Výpočet je prováděn následujícím způsobem: Nejprve se vytvoří model prutu, tj. množina hmotných kloubů vzájemně propojených soustavou pružin. Osa prutu je rovnoběžná s osou x souřadného systému. Počáteční podmínky jsou nastaveny tak, že model odpovídá nenapjatému prutu v klidu (rychlosti hmotných kloubů jsou nulové). Na konci prutu – páru hmotných kloubů – je vložena dvojice nekonzervativních sil působících kolmo na dílec. Síly tedy sledují aktuální normály dílce v místě působení. Dvojice sil na jednom konci prutu vytváří kroutící moment opačný, než dvojice sil na druhém konci. Následně je spuštěn výpočet s vhodným časovým krokem.
Na obr. 3 jsou zobrazeny důležité fáze simulace pro kroutící moment M = 3Mcr. Konečným stavem je stabilní smyčka těsně před vznikem kontaktu částí prutu.
a) počáteční stav
b) prut při maximální rotaci
c) klidový stav těsně před ztrátou stability
d) probíhá vybočení prutu
e) stabilní stav
Obr. 3: Fáze simulace kroucení prutu při kroutícím momentu M = 3Mcr
5 Bifurkační bod
Simulace, jejíž důležité fáze jsou vidět na obr. 3, ukázala, že model je s to vystihnout destabilizaci prutu při kroucení. Zajímavostí je příčina ztráty symetrie úlohy. Kdyby totiž byl model včetně počátečních podmínek přesně symetrický, nemohlo by k vybočení prutu dojít. Původ nesymetrie v modelu lze vysledovat k nesymetrické poloze v souřadném systému, viz obr. 2, a dále k nepřesným operacím s čísly s pohyblivou desetinou čárkou.
Z vlastností úlohy je zřejmé, že prut může vybočit dvěma směry, jak je vidět na obr. 3c (tj. nahoru nebo dolů). Situace je opět obdobou vzpěru prutu. Tuto možnost vybočení prutu oběma směry potvrdily další simulace s odlišnými parametry. Tedy směr, kterým dokonale symetrický prut vybočí, je za daných okolností typicky nepředpověditelný.
Pro ověření správnosti výsledků simulace byl proveden výpočet bifurkačního diagramu, viz obr. 4. Diagram byl sestaven pro proměnlivý kroutící moment M, přičemž se vynášela hodnota vzepětí prutu 
. Vzepětím prutu se myslí vzdálenost mezi spojnicí konců a průřezem v polovině prutu (měřeno v ose). V diagramu je vzepětí přepočítáno do bezrozměrného tvaru (L je délka nazatíženého prutu).
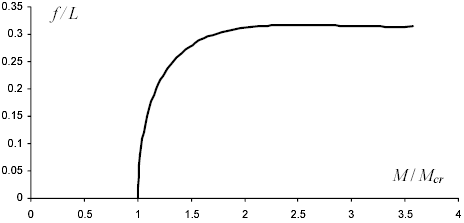
Obr. 4: Bifurkační diagram
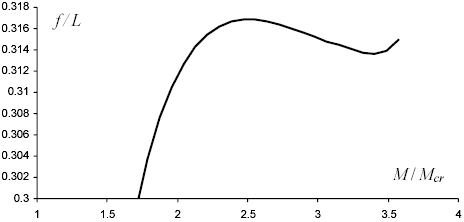
Obr. 5: Detail zakončení bifurkačního diagramu
Z bifurkačního diagramu je patrné, že se jedná o stejný typ bifurkačního bodu jako u vzpěru prutu – superkritickou vidličkovou bifurkaci. V diagramu je kromě tohoto bifurkačního bodu, kde platí M = Mcr, ještě jeden kritický bod, nalézající se na konci spojnice, kde přibližně platí M = 3.57 Mcr. Při dosažení druhého kritického bodu dochází k další ztrátě stability. Tento okamžik odpovídá „snaze o zavinutí smyčky“. Protože ale zvolený model nepodporuje kontakt částí prutu, tak překročení tohoto bodu již nevede k získání stabilního statické stavu. Obrázek 5 ukazuje detail diagramu v okolí druhého kritického bodu.
6 Závěr
V článku byl prezentován nelineární model pro výpočet kroucení dokonale symetrického štíhlého prutu, který dokázal vystihnout jev ztráty stability. Dle očekávání tato ztráta stability probíhá obdobně jako v případě vzpěru prutu – dochází k superkritické vidličkové bifurkaci.
Simulací se rovněž prokázalo, že kroucení umožňuje vznik stabilní smyčky. Autorem dříve studované jednoduché úlohy produkovaly jen smyčky nestabilní, viz např. [3].
Zajímavým se ukázal proces ztráty stability. Při plném kroutícím momentu se nejprve realizuje zkrucování prutu bez příčného vybočení, ke kterému dojde až po ustálení pohybu, viz obr. 3. Pohyb prutu (kroutivé kmitání) zřejmě zabraňuje příčné destabilizaci.
Za zmínění rovněž stojí problematika nanesení nekonzervativních dvojic sil a dále problém zachycení prutu v prostoru. Dle definice sil v modelu totiž dochází k mírnému porušení podmínky dvojice sil – síly nesdílí společnou rovinu. Vlivem tohoto jevu těžiště prutu mění polohu v prostoru. Nabízejí se dvě možná řešení: nesnadné zachycení prutu pomocí vhodných podpor, nebo zajištění splnění porušené podmínky dvojice sil.
Poděkování
Článek vznikl za přispění dotace podle rozhodnutí MŠMT č. 52130/2005 k návrhu výzkumného záměru MSM0021630504.
Literatura
[1] Arnold, V. I., TEÓRIA KATASTROF (orig. TEORIJA KATASTROF, vydavatelstvo Moskevské univerzity 1983), vydavateľstvo Alfa, Bratislava 1986
[2] Henrych, J., ÚPLNÁ SOUSTAVA FINITNÍCH METOD MECHANIKY A MOŽNOSTI DALŠÍHO ROZVOJE, studie ČSAV 6.85, nakladatelství Akademia, Praha 1985
[3] Frantík, P., STABILITY STUDY OF THE ELASTIC LOOP, 5th International PhD Symposium in Civil Engineering, Delft 2004, Netherlands