OHYBOVÉ PORUŠENÍ BETONU S VLÁKNY: MODEL A JEHO APLIKACE

P. Frantík1, Z. Keršner2

1Ing. Petr Frantík, Ph.D., Ústav stavební mechaniky, Fakulta stavební, Vysoké učení technické v Brně, Veveří 331/95, 602 00 Brno, Česká republika, e-mail: kitnarf at centrum dot cz
2Ing. Zbyněk Keršner, CSc., Ústav stavební mechaniky, Fakulta stavební, Vysoké učení technické v Brně, Veveří 331/95, 602 00 Brno, Česká republika, e-mail: kersner.z at fce.vutbr dot cz

 

Abstrakt
Concrete is quasi-brittle material. Three point bending test of central notched specimen is usually used for determination of fracture properties of concrete with/without fibres. Fibres improve these properties. An approximation of bending fracture model of recorded l-d diagram is used here for estimation and modelling of fracture behaviour of tested material.

 

1 ÚVOD

Beton patří mezi tzv. kvazikřehké stavební materiály. Stupeň křehkosti/tažnosti lze u tohoto materiálu kvantifikovat řadou lomových charakteristik, určovaných příslušnými zkouškami. Častou konfiguraci zkoušky představuje tříbodový ohyb vzorku/trámce s centrálním zářezem při taženém okraji. Pokud provádíme zatěžování přírůstkem posunu, můžeme obdržet závislost zatížení-posun včetně tzv. tahového změkčení, tedy včetně sestupné větve diagramu po dosažení maximální úrovně zatížení. Pro zlepšení vlastností prostého betonu – snížení jeho křehkosti – lze do betonové směsi přidat vlákna vybraného druhu. Takováto vlákna mohou při probíhajícím lomu omezovat šíření mikrotrhlin/trhlin.

Přídavek vláken ovlivňuje chování vzorků při zmíněné zkoušce. Lze toto chování výstižně modelovat a předpovídat při různých druzích a dávkách vláken? Odpověď na tuto otázku se pokouší nalézt mnoho výzkumných pracovišť [3]. Tento příspěvek ukazuje možnosti dříve vyvinutého modelu lomu při ohybu [2]. Model je aplikován na diagramy zatížení-průhyb tří sérií vzorků: z prostého betonu, z drátkobetonu a z betonu s vlákny Forta Ferro (bylo využito experimentů doc. Vodičky z FSv ČVUT v Praze).

 

2 MODEL LOMU PŘI OHYBU

Pro zjednodušené modelování zkoušky tříbodovým ohybem trámce s centrálním zářezem se aplikoval jednoduchý model lomu při ohybu [2]. Trámec je v modelu nahrazen tuhou deskou připevněnou pomocí kloubu a dvou sad tahových vláken k tuhé stěně, která tvoří osu symetrie úlohy. Předpokládejme, že každá sada vláken může zastupovat jeden z materiálů, tj. beton nebo vlákna.

Funkce napjatosti vlákna je zvolena s lineární vzestupnou a sestupnou větví, viz obr. 1. Funkci jednoznačně určují tři vybrané lokální parametry vlákna: počáteční tuhost vlákna kincr,i, maximální tahová síla Fpeak,i, kterou vlákno přenese, a koeficient přetvárné práce ci, jenž vyjadřuje podíl celkové přetvárné práce nutné pro „přetržení“ vlákna a přetvárné práce nutné pro dosažení maximální síly ve vláknu.


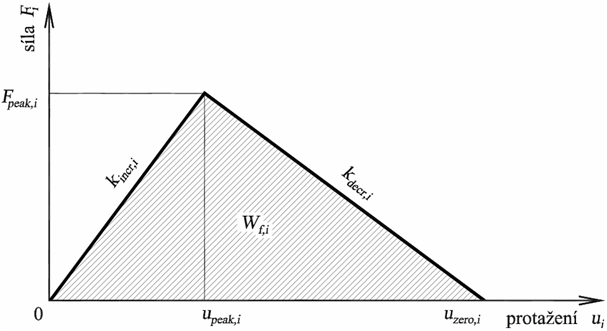
Obr. 1 Funkce napjatosti i-tého vlákna

Lokální parametry vlákna nejsou vzhledem k diskrétnímu charakteru modelu vhodné pro jeho parametrizaci. Proto jsou definovány globální parametry modelu: pevnost v tahu ft, tuhost v tahu kt a koeficient přetvárné práce c, které byly do modelu zahrnouty pomocí vztahů:

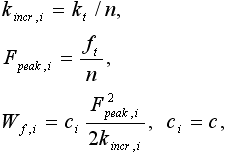(1)

kde n je počet vláken a Wf,i označuje celkovou přetvárnou práci potřebnou pro „přetržení“ vlákna. Z uvedených vztahů je patrné, že proměnlivost parametrů po výšce se neuvažuje. Připomeňme, že globální parametry kt, ft a c se vyskytují dvakrát pro dvě různé sady vláken. Sady vláken dále rozlišujme římskými číslicemi uváděnými u symbolů horním indexem. Pro specifikaci modelu betonu s vlákny tedy potřebujeme znát šestici globálních parametrů: ktI, ftI, cI a ktII, ftII, cII.

 

3 APROXIMACE DIAGRAMŮ ZATÍŽENÍ-POSUN

Diagramy zatížení-posun (l-d diagramy) získané z měření na trámcích všech tří sérií byly podrobeny nejprve transformaci pro snížení počtu bodů (řádově tisíce). Transformace byla provedena trasováním křivky ve zvoleném měřítku tak, aby vzdálenost výsledných bodů byla přibližně konstantní (vzdálenost bodů závisí na zvoleném měřítku). Tato transformace se negativně projevuje na zobrazení l-d diagramů vzorků z prostého betonu, viz obr. 3 až 5.

Transformovaná bodová pole změřených l-d diagramů se poté užila k odhadu šestice parametrů modelu pomocí genetických algoritmů [1]. Model měl pro jednoduchost geometrické rozměry nastavené jako jednotkové. Lze prokázat, že odezva modelu je na geometrii lineárně závislá. Kritériem aproximace byla zvolena chyba nejmenších čtverců. Opakované spouštění genetických algoritmů s náhodnými počátečními hodnotami ukázalo výskyt více řešení.

Existence více řešení

Výskyt více lokálních minim chyby aproximace byl vzhledem k silné nelinearitě problému očekáván zejména u sérií vzorků s vlákny. Překvapující byla nejednoznačnost řešení u vzorků z prostého betonu, kde se očekávalo, že zdvojení sad vláken způsobí pouze zlepšení výstižnosti naměřených l-d diagramů. K nejvýraznějším rozdílům v nalezených řešeních docházelo u vzorků třetí série s aplikovanými vlákny Forta Ferro, což je vzhledem k tvaru zatěžovacích diagramů pochopitelné (viz obr. 2). Dvojici nalezených řešení aproximace lze porovnat na obr. 2 a jim odpovídající parametry modelu uvádí tabulka 1.


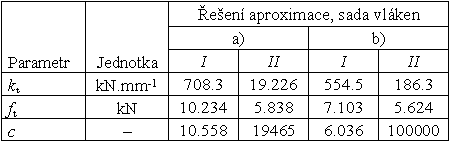
Tab. 1 Srovnání vypočtených parametrů modelu pro dvě řešení aproximace l-d diagramu z třetí série: vlákna Forta Ferro ff1703l2, viz obr. 2


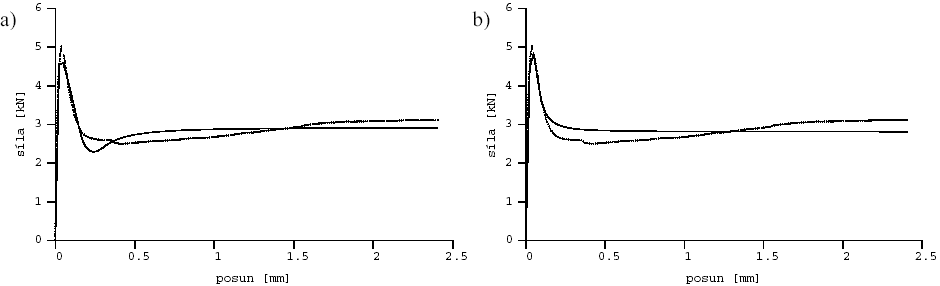
Obr. 2 Srovnání dvou odlišných řešení aproximace l-d diagramu z třetí série: vlákna Forta Ferro ff1703l2

Ze srovnání dvou řešení na obr. 2 je patrné, že model v případě a) vystihnul zejména dvě lokální maxima naměřeného zatěžovacího diagramu. V případě b) model nevykazuje přítomnost dvou lokálních maxim, ovšem velmi dobře vystihuje oblast při dosažení prvního lokálního maxima. Vypočtené parametry modelu pro tyto dva případy (Tab. 1) ukazují, že dosažení dvou lokálních maxim – případ a) – souvisí s dominancí absolutních hodnot parametrů kI a cII. V případě b) již dominance parametru kI není tak výrazná, což má za důsledek absenci druhého lokálního maxima. Význam hodnot parametrů lze lépe poznat z obr. 11.

Výsledné aproximace

Vzhledem k výše popsané víceznačnosti řešení aproximace byla s ohledem na možnosti vybírána taková řešení, která „nejlépe odpovídají“ pojetí vláknového kompozitu, respektive prostému betonu. Například z dvou řešení aproximace, která byla popsána v předchozí části, lépe odpovídal případ a). Na obrázcích 3 až 10 jsou zobrazeny výsledné aproximace včetně transformovaných bodů změřených zatěžovacích diagramů.


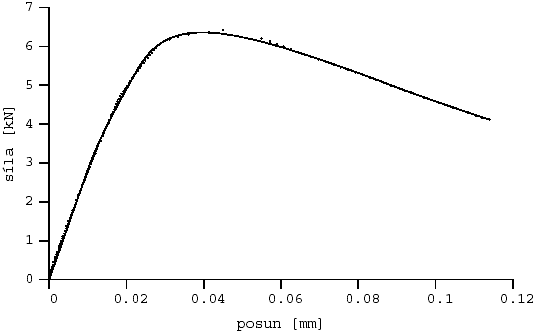
Obr. 3 Aproximace l-d diagramu z první série: prostý beton pb1503l1



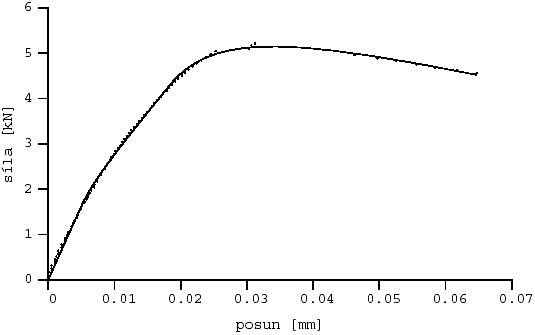
Obr. 4 Aproximace l-d diagramu z první série: prostý beton pb1503l2



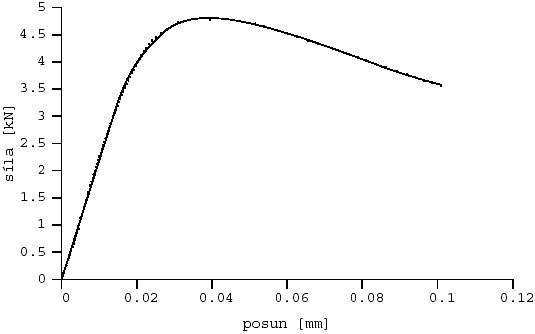
Obr. 5 Aproximace l-d diagramu z první série: prostý beton pb1503l3



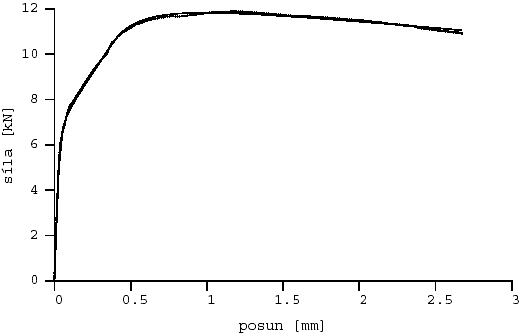
Obr. 6 Aproximace l-d diagramu z druhé série: drátkobeton dr2203l1



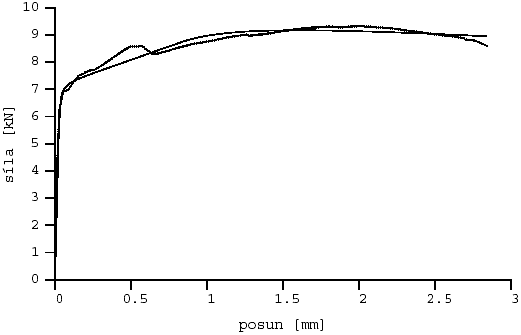
Obr. 7 Aproximace l-d diagramu z druhé série: drátkobeton dr2203l2



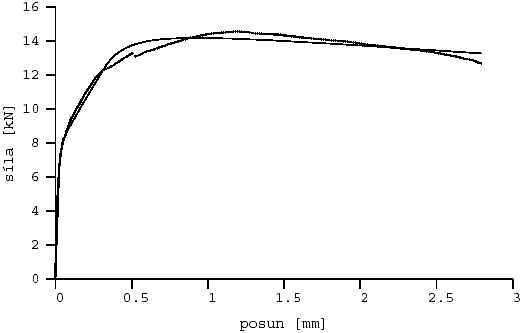
Obr. 8 Aproximace l-d diagramu z druhé série: drátkobeton dr2203l3



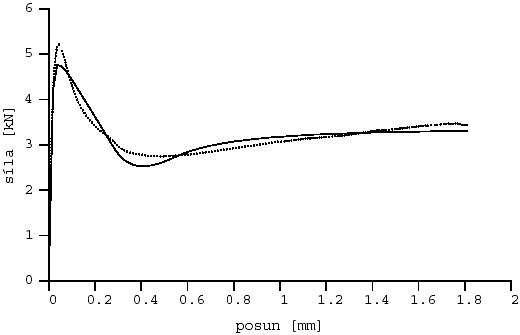
Obr. 9 Aproximace l-d diagramu z třetí série: vlákna Forta Ferro ff1703l1



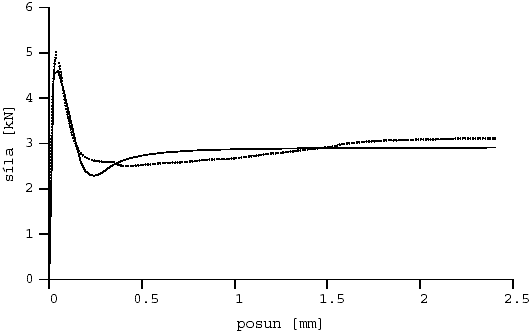
Obr. 10 Aproximace l-d diagramu z třetí série: vlákna Forta Ferro ff1703l2

Shrnutí výsledků aproximace

Obrázek 11 shrnuje tahové diagramy vždy dvou sad vláken modelu, odpovídající vybraným aproximacím (viz obrázky 3 až 10): plná čára je přiřazována sadě vláken „betonu“, čárkovaná čára sadě reprezentující reálná vlákna. Připomeňme, že tyto diagramy odpovídají modelu s jednotkovou geometrií. Parametry popisující uvedené tahové diagramy jsou pro jednotlivé série vzorků uvedeny v tabulkách 2 až 4.


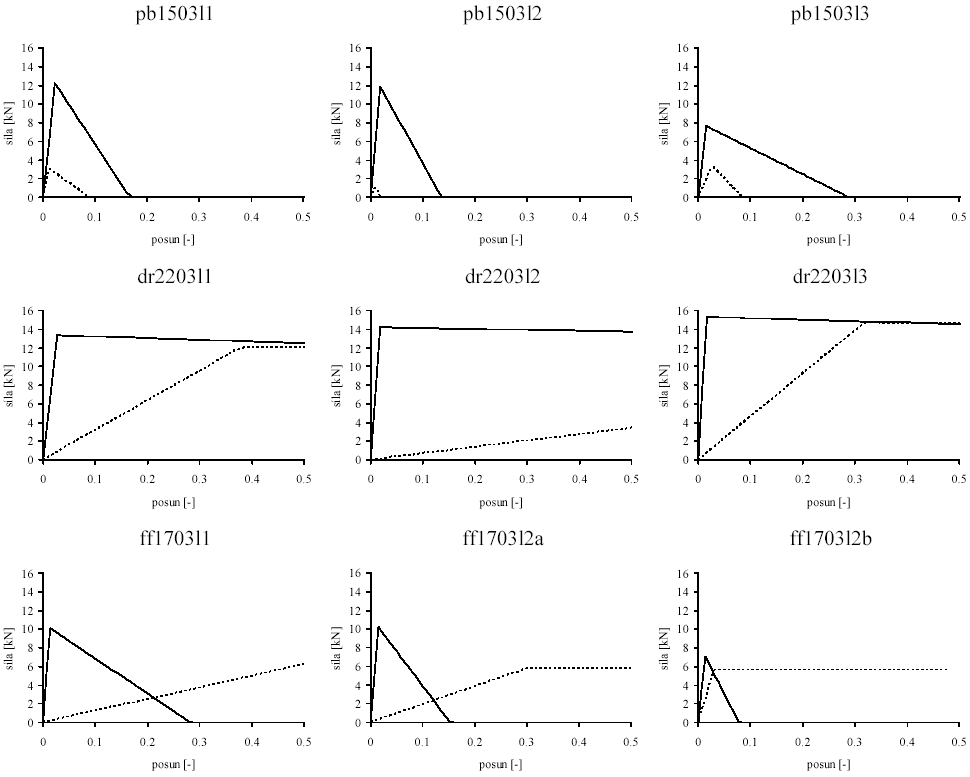
Obr. 11 Diagramy l-d, odpovídající dvěma materiálům



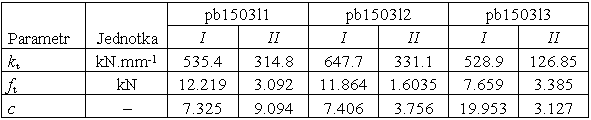
Tab. 2 Parametry modelu pro l-d diagramy z první série: prostý beton



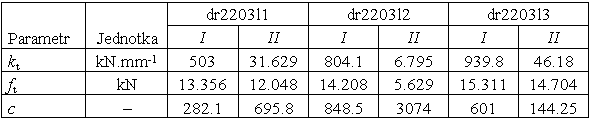
Tab. 3 Parametry modelu pro l-d diagramy z druhé série: drátkobeton



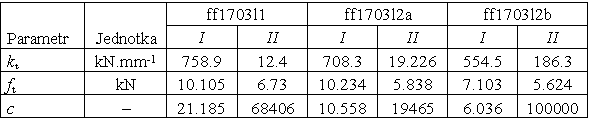
Tab. 4 Parametry modelu pro l-d diagramy ze třetí série: vlákna Forta Ferro

 

4 ZÁVĚR

Z uvedených výsledků výpočtů se ukázalo, že může být obtížné (popřípadě nemožné) rozeznat příslušnost výpočtových sad vláken I a II k betonu, resp. k reálným vláknům – viz tahové diagramy modelu pro aproximaci l-d diagramů vzorků z drátkobetonu v obrázku 11. V některých případech dochází při aproximaci k výběru takového řešení, kterému zřejmě nelze přiřadit představu rozdělení na beton a vlákna.

Dále se ukazuje, že model umožňuje výskyt více řešení (i více než tří výstižných), mezi kterými je obtížné rozhodnout.
U l-d diagramů vzorků s vlákny Forta Ferro nebylo dosaženo uspokojivě výstižných řešení vzhledem k druhým dvěma sériím.

 

PODĚKOVÁNÍ

Tento výsledek byl získán za finančního přispění MŠMT, projekt 1M6840770001, v rámci činnosti výzkumného centra CIDEAS. Při řešení byly částečně využity teoretické výsledky dosažené v projektu GA ČR 103/03/1350.

 

LITERATURA

[1] Cacka, P. Vícekriteriální genetické algoritmy. Diplomová práce, Ústav automatizace a informatiky FSI VUT v Brně, 2003.

[2] Frantík, P. Jednoduchý model lomu trámce. Sborník semináře Problémy lomové mechaniky IV., IFM AV ČR a STM FAST VUT v Brně, 2004, 21–27.

[3] Shah, S. P. (2002) High Performance Concrete: Strength vs. Ductility and Durability. Sborník Non-Traditionmal Cement and Concrete, Bílek & Keršner (eds.), Brno, 347–358.