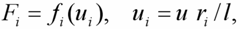
*Ing. Zbyněk Keršner, CSc.: Ústav stavební mechaniky, FAST VUT v Brně; Veveří 331/95; 602 00 Brno; tel: +420.541 147 362; e-mail: kersner.z at fce.vutbr dot cz
**Ing. Petr Frantík, Ph.D.: Ústav stavební mechaniky, FAST VUT v Brně; Veveří 331/95; 602 00 Brno; tel: +420.541 147 376;
e-mail: kitnarf at centrum dot cz
***Ing. Ladislav Řoutil: Ústav stavební mechaniky, FAST VUT v Brně; Veveří 331/95; 602 00 Brno; tel: +420.541 147 131;
e-mail: routil.l at fce.vutbr dot cz
****Ing. Václav Veselý, Ph.D.: Ústav stavební mechaniky – CIDEAS, FAST VUT v Brně; Veveří 331/95; 602 00 Brno;
tel: +420.541 147 362; e-mail: vaclav_vesely at centrum dot cz
Summary: Three point bending test of central notched specimen is used for determination of fracture properties of concrete, mortar and hardened cement paste. The properties – e.g. effective fracture toughness and effective crack length, fracture energy and also modulus of elasticity – are calculated on the base of load-deflection (l-d) diagrams from mentioned test.
An approximation of model of recorded l-d diagram is possible to use for estimation of these properties, which can serve as input values for numerical modelling of fracture. The model – bending fracture model – of l-d diagrams obtained from experiments is introduced in this paper.
1. Úvod
V posledních třech (až čtyřech) dekádách se v mnoha zemích ve výzkumu i v praxi podporuje zavedení přístupů lomové mechaniky do návrhu konstrukcí z prostého i vyztuženého betonu. Že tato podpora není masivní v České republice zůstává s podivem, neboť tento krok slibuje mnohé: významný ekonomický přínos, dosažení jednotných návrhových pravděpodobností poruchy pro konstrukce různých rozměrů a potažmo zvýšení jejich spolehlivosti, jakož i možnost použití nového způsobu navrhování a nových druhů betonu (např. s vysokými pevnostmi, s vysokými užitnými vlastnostmi, s vlákny apod.) – viz kupř. tradiční opory: Karihaloo (1995), Bažant & Planas (1998).
Podpora se nicméně objevuje v oblasti modelování konstrukcí ze zmíněných materiálů, které se pro věrné vystihnutí chování konstrukcí/prvků i při šíření trhlin a při odhadu kolapsu neobejde bez tzv. lomových charakteristik. Existuje jich celá řada a zorientovat se v nich v tuzemských podmínkách pro třídu těchto tzv. kvazikřehkých materiálů bylo jedním z cílů řešení disertačních prací na pracovišti autorů – viz Veselý (2004), Stibor (2004).
Ke stanovování některých lomových charakteristik betonu, malty či zatvrdlé cementové pasty lze užít několik konfigurací lomových testů. K těm „dobře zvládnutým“ patří zkouška tříbodovým ohybem vzorků ve tvaru trámců s centrálním zářezem v tažených vláknech. Při tomto testu se zaznamenává závislost zatížení a odpovídajícího průhybu uprostřed rozpětí – získává se tzv. l-d diagram; zatěžování se provádí s řízeným přírůstkem deformace. K typickým výstupům této zkoušky – vyhodnocením zmíněného l-d diagramu – patří lomová houževnatost (resp. její efektivní hodnota a kritická délka efektivní trhliny), houževnatost, charakteristická délka kompozitu apod., z těch využitelných při modelování (např. pomocí MKP softwaru ATENA) je to především tzv. lomová energie a také modul pružnosti.
Pro účely vyhodnocení testy získaných l-d diagramů bývá užitečné jejich průběhy různými modely nahrazovat – viz např. Barr & Lee (2003), resp. Řoutil & Lehký (2004), Řoutil (2004), Frantík et al. (2004) či Řoutil et al. (2005). V předkládaném příspěvku se pozornost zaměřuje na aproximace tzv. jednostupňového modelu lomu při ohybu s využitím experimentálně získaných l-d diagramů. Myšlenka tohoto modelu se poprvé objevuje v článku Frantík (2004).
2. Jednostupňový model lomu při ohybu
Pro zjednodušené modelování zkoušky tříbodovým ohybem trámce s centrálním zářezem byl vyvinut jednoduchý model lomu v souladu s přístupem minimalizace stupňů volnosti úlohy. V tomto modelu se předpokládá, že postačuje detailněji vystihnout pouze oblast na ose symetrie úlohy a dále, že je možno ohýbající se nosník redukovat na tuhou desku otáčející se na pevně daném kloubu, situovaném při okraji trámce, viz obr. 1.
Obrázek 1 Zjednodušený model lomu trámce při ohybu.
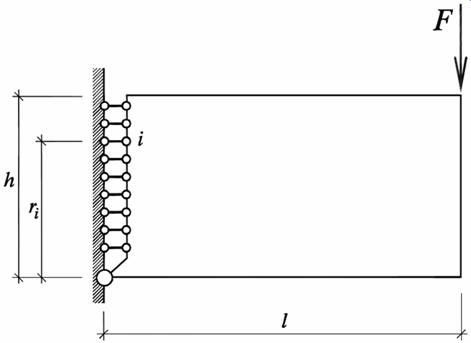
Obrázek 1 představuje schéma modelu: tuhá deska reprezentující polovinu trámce je připevněna pomocí kloubu a tahových vláken k tuhé stěně, která tvoří osu symetrie úlohy. Pro funkčnost modelu je rozhodující působení tahových vláken. Definujme sílu Fi kterou i-té vlákno působí na tuhou desku pomocí vztahu:
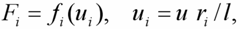| (1) |
kde fi je funkce napjatosti i-tého vlákna, ui je protažení vlákna, ri je rameno vlákna (viz obr. 1), u je průhyb trámce a l je polovina rozpětí trámce. Funkce napjatosti vlákna fi byla zvolena s lineární vzestupnou i sestupnou větví, viz obr. 2. Funkci jednoznačně určují tři vybrané lokální parametry vlákna: počáteční tuhost vlákna kincr,i, maximální tahová síla Fpeak,i, kterou vlákno přenese a koeficient přetvárné práce ci, jenž vyjadřuje podíl celkové přetvárné práce nutné pro „přetržení“ vlákna a přetvárné práce nutné pro dosažení maximální síly ve vláknu.
Lokální parametry vlákna nejsou vzhledem k diskrétnímu charakteru modelu vhodné pro parametrizaci modelu. Proto jsou definovány globální parametry modelu: pevnost v tahu ft, tuhost v tahu kt a koeficient přetvárné práce c, které lze do modelu zahrnout pomocí vztahů:
 | (2) |
kde n je počet vláken, h je výška průřezu trámce v místě zářezu, ri je rameno i-tého vlákna (viz obr. 1), nff je počet bázových funkcí reprezentujících variabilitu vlastností vláken po výšce průřezu trámce, Aft,j je amplituda j-té bázové funkce,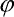 
ft,j je fázové posunutí j-té bázové funkce a Wf,i je celková přetvárná práce potřebná pro „přetržení“ vlákna. Pro zvolený počet bázových funkcí nff lze amplitudy Aft,j a fáze 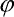ft,j bázových funkcí chápat také jako globální parametry modelu, jelikož nezávisle na počtu vláken definují rozložení jejich tahové pevnosti Fpeak,i.
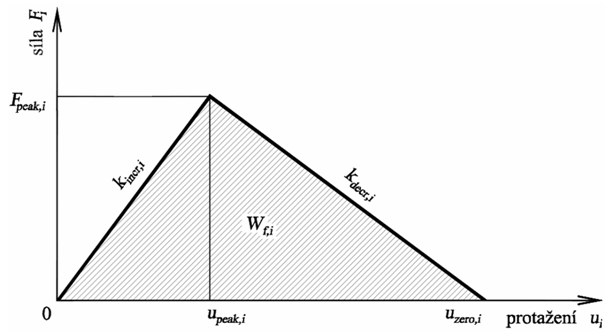
Obrázek 2 Funkce napjatosti i-tého vlákna.
Jsou-li dány rozměry trámce a globální parametry modelu, pak lze l-d diagram stanovit pomocí vztahu:
 | (3) |
kde F je zatěžující síla pro daný průhyb trámce u.
3. Aplikace modelu
Možnosti výše představeného modelu byly testovány na sadě dříve získaných l-d diagramů. Šlo o šest vzorků z betonu pro výrobu pražců (označení B1 až B6), které byly podrobeny zkoušce tříbodovým ohybem trámců se zářezem a výsledky analyzovány a publikovány – pro podrobnosti viz Veselý & Stibor (2002), resp. Veselý (2004), Stibor (2004).
Tyto l-d diagramy z experimentů posloužily při aproximaci modelu, přičemž byl zvolen počet vláken n = 40 a počet bázových funkcí nff = 5. Globální parametry kt, ft, c, Aft,1-5, 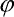ft,1-5, viz vztahy (3), byly hledány pomocí jednokriteriálních genetických algoritmů – Cacka (2003) – s kritériem minima chyby nejmenších čtverců. Poznamenejme ještě, že vzhledem k náročnosti aproximace byla provedena transformace bodového pole pro snížení počtu vstupních dat. Této transformaci nevyhověl vzorek B5 z důvodu výrazné skokové změny funkčních hodnot, a proto byl vyřazen.
Vizuální srovnání příslušných l-d diagramů s jejich aproximovanými modely umožňuje sada obrázků 3 až 7 pro zkoušky B1, B2, B3, B4 a B6. Shoda předkládaných experimentálních l-d diagramů s modelem se jeví jako mimořádně dobrá, nezasvěcený čtenář by mohl model považovat spíše za spojnici naměřených bodů zatížení-průhyb. V tabulce 1 lze nalézt parametry použitého modelu s jejich aproximovanými hodnotami pro pět zmíněných výsledků experimentů. Objektivním měřítkem úspěšnosti aproximace může být průměrná chyba nejmenších čtverců err, uvedená rovněž v tabulce 1.
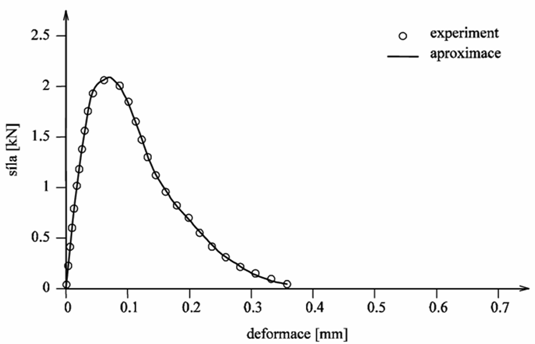
Obrázek 3 Aproximace modelu pomocí vybraných bodů l-d diagramu: test B1.
Obrázek 4 Aproximace modelu pomocí vybraných bodů l-d diagramu: test B2.
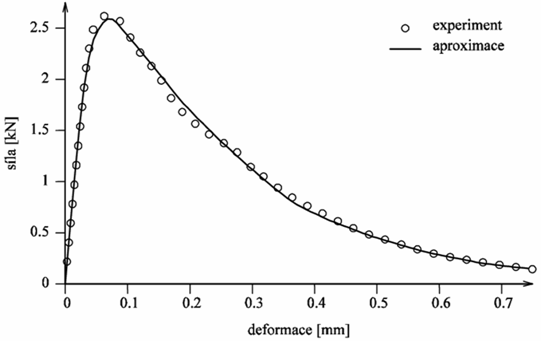
Obrázek 5 Aproximace modelu pomocí vybraných bodů l-d diagramu: test B3.
Obrázek 6 Aproximace modelu pomocí vybraných bodů l-d diagramu: test B4.
Obrázek 7 Aproximace modelu pomocí vybraných bodů l-d diagramu: test B6.
Tabulka 1 Nalezené parametry modelu a průměrná chyba aproximace err.
4. Závěr
Jednostupňový model lomu trámce ohybem s aplikací jednokriteriálních genetických algoritmů představuje účinný nástroj pro popis diagramů zatížení-průhyb při lomové zkoušce. Výše popsaný postup lze s výhodou použít pro transformace experimentálně získaného l-d diagramu do "výpočtového" l-d diagramu, z něhož se určují lomové parametry podle zavedených metod. Při zkoušce je nutno snímat monitorované veličiny (zatížení, průhyb) ve velmi krátkých časových intervalech, aby mohly být zachyceny náhlé jevy (např. rychlé rozšíření trhliny projevující se skokem na zatěžovacím diagramu). Výsledkem je pak složitá zatěžovací závislost daná jako množina velkého množství bodů. Pro zpracování těchto diagramů za účelem stanovení lomových parametrů je naopak výhodné použití co nejjednodušší křivky. Naznačeným postupem lze „vyhladit“ naměřené l-d diagramy bez významné ztráty přesnosti – hodnota chyby aproximace modelu je velmi malá (řádově setiny kN), což potvrzuje těsnou shodu experimentu a modelu při optickém srovnání.
5. Poděkování
Práce na tomto příspěvku byly podporovány z prostředků projektu GA ČR 103/03/1350.
6. Literatura
Barr, B. & Lee, M. K. (2003) Modelling the strain-softening behaviour of plain concrete using a double-exponential model. Magazine of Concrete Research, 4, 343–353.
Bažant, Z. P. & Planas, J. (1998) Fracture and Size Effect in Concrete and other Quasibrittle Materials. CRC Press, Boca Raton, Florida.
Cacka, P. (2003) Vícekriteriální genetické algoritmy. Diplomová práce, ÚAI FSI VUT v Brně.
Frantík, P. (2004) Jednoduchý model lomu trámce. Sborník semináře Problémy lomové mechaniky IV., ÚFM AV ČR a STM FAST VUT v Brně, 21–27.
Frantík, P., Keršner, Z. & Řoutil, L. (2004) Aplikace 2e modelu: modifikace určení parametrů. Sborník konference Experiment – významný zdroj poznání a verifikace metod navrhování nosných stavebních konstrukcí, Brno, 97–100.
Karihaloo, B. L. (1995) Fracture mechanics of concrete. Longman Scientific & Technical, New York.
Řoutil, L. (2004) Modelování chování předpjatého pražce při kontrolní zkoušce s uvažováním variability vstupních parametrů, především lomových. Diplomová práce, STM FAST VUT v Brně.
Řoutil, L., Kutín, A., Frantík, P., Lehký, D., Matesová, D. & Keršner, Z. (2005) Určení lomově-mechanických vstupů pro numerické modelování. CD sborník Aplikovaná mechanika 2005, Hrotovice.
Řoutil, L. & Lehký, D. (2004) Metody stanovení parametrů dvouexponenciálního modelu l-d diagramu. Sborník semináře Problémy lomové mechaniky IV., ÚFM AV ČR a STM FAST VUT v Brně, 74 –80.
Stibor, M. (2004) Lomové parametry betonu a jejich určování. Disertační práce, STM FAST VUT v Brně.
Veselý, V. (2004) Parametry betonu pro popis lomového chování, Disertační práce, STM FAST VUT v Brně.
Veselý, V. & Stibor, M. (2002) Efektivní lomové parametry betonu pro železniční pražce. CD sborník konference Inženýrská mechanika, Svratka.