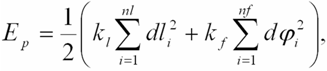

1Ing. Petr Frantík, Ph.D.: Ústav stavební mechaniky; Fakulta stavební; Vysoké učení technické v Brně; Veveří 331/95; 602 00 Brno; e-mail: kitnarf at centrum dot cz
Summary: Hypothesis about dynamical process of stability loss of high symmetrical von Misses truss in the state of unsymmetrical stress is verified by simulation of discrete nonlinear dynamical system. Unsymmetrical stress means possible unsymmetrical postcritical shape of von Misses truss.
1. Úvod
V současnosti se můžeme ve vědeckých kruzích běžně setkat s prováděním výpočtů mnohdy velmi komplexních nelineárních modelů. Ačkoliv jsou složitosti možného chování nelineárních systémů do značné míry odkryty, zanedbává se většinou z praktických důvodů podrobnější analýza „správnosti“ nalezených řešení. Jednou z vlastností nelineárních systémů je obecně např. současný výskyt více stabilních statických stavů, které jsou často spojeny s existencí nestabilních statických stavů, jejichž rozpoznání může být pro statické výpočetní metody problémem.
Výhodou, kterou máme k dispozici při analýze nelineárních systémů, je v souvislosti se znalostí jejich tzv. generických vlastností povědomí, že složitost jejich chování lze ilustrovat i na velmi jednoduchých modelech. Jedním z takových modelů je i vzpěradlo, známé spíše jako von Missesův nosník, viz Bažant & Cedolin (1991). Vzpěradlo je jednoduchá prutová konstrukce, znázorněná včetně užitého označení na obr. 1.
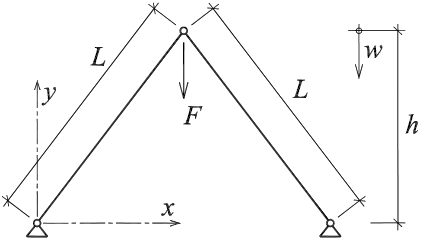
Obr. 1 Schematické znázornění vzpěradla – von Missesova nosníku
Mějme vysoké, dokonale symetrické vzpěradlo, skládající se ze dvou velmi štíhlých prutů z pružného materiálu, které vybočují v rovině vzpěradla. Pak existuje mnoho statických stavů, kterých může být při jeho deformaci dosaženo. Tyto stavy a jejich existence jsou podrobně popsány v publikaci Frantík (2004.1), kde je ukázán výskyt v zásadě dvou druhů pokritického působení vzpěradla: symetrické a nesymetrické napjatosti, viz obr. 2.
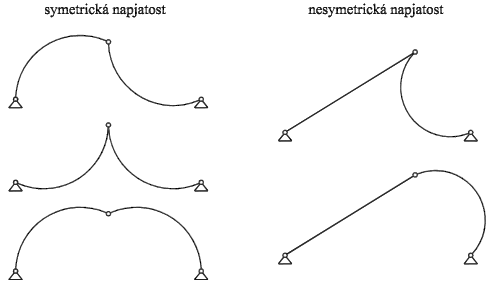
Obr. 2 Možné pokritické stavy vzpěradla bez svých symetrických protějšků
Symetrická napjatost vzpěradla je statickým stavem, jenž se vyskytuje pro vzpěradla libovolného poměru h/L, kde h je výška vzpěradla a L je délka jeho prutů, přičemž platí h < L. Jinak tomu je u nesymetrické napjatosti, jejíž existence souvisí s výškou vzpěradla. Minimální výška vzpěradla s výskytem nesymetrické napjatosti byla vypočtena za předpokladu zanedbání normálového protažení prutů hmin = 0.5774 L, viz Frantík (2004.1). Existence nesymetrické napjatosti (ve smyslu statického stavu) je navíc obecně omezena polohou středního kloubu vzpěradla, viz obr. 3 pro vzpěradlo h = 0.8 L.
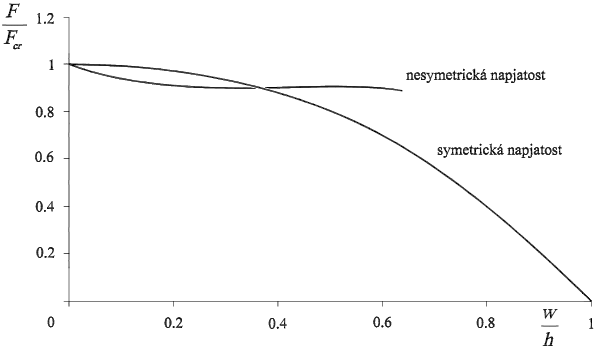
Obr. 3 Závislost síly F působící ve středním kloubu na jeho svislém posuvu w pro vzpěradlo h = 0.8 L (Fcr je kritická síla vzpěradla, tj. síla F nutná pro ztrátu stability prutů vzpěradla)
Na obr. 3 je vidět závislost síly F, nutné pro udržení vybraného statického stavu, na poloze středního kloubu vzpěradla (specifikované svislým posuvem w, viz obr. 1) pro vzpěradlo h = 0.8 L (převzato z Frantík (2004.1)). Z grafu je patrné, že výskyt nesymetrické napjatosti končí při posuvu přibližně wmax = 0.637 h.
2. Úloha
V návaznosti na výše popsaná fakta se soustřeďme na nalezení způsobu, jakým probíhá deformace vzpěradla. Pro zjednodušení problému se věnujme pouze vzpěradlu h = 0.8 L, přičemž jej budeme zatěžovat přírůstkem svislého posunu středního kloubu (jedná se o pokritickou úlohu). Pro tyto účely byl sestaven model schematicky znázorněný na obr. 4.
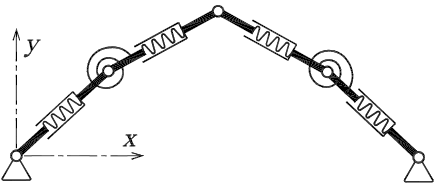
Obr. 4 Schematické znázornění diskrétního modelu vzpěradla
Pruty vzpěradla jsou rozděleny na určitý počet stejně dlouhých dílců s vnitřní pružinou (umožňující normálové protažení) vzájemně spojených klouby s rotačními pružinami. Oba typy pružin jsou uvažovány jako lineární. Potenciální energii Ep, která se akumuluje v těchto pružinách lze zapsat ve tvaru:
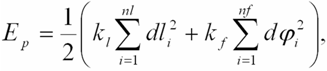 | (1) |
kde nl je počet normálových pružin, nf je počet rotačních pružin, kl je tuhost normálových pružin, kf je tuhost rotačních pružin,
dli je protažení i-tého dílce a d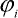 je natočení rotační pružiny (vzájemné pootočení dílců, které pružina spojuje). Uvažujme,
je natočení rotační pružiny (vzájemné pootočení dílců, které pružina spojuje). Uvažujme,
že deformační stav modelu vzpěradla jednoznačně určují polohy všech jeho kloubů. Nechť je poloha každého kloubu dána dvojicí souřadnic ( xi , yi ), kde i je index kloubu. Pro protažení normálové pružiny dli lze pak psát:
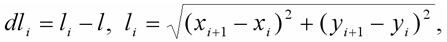 | (2) |
kde l je původní délka dílce (dílec bez napětí) a li je délka dílce po deformaci. Pro pootočení rotační pružiny d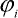 lze psát:
lze psát:
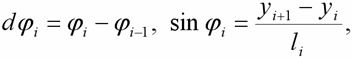 | (3) |
kde  je pootočení i-tého dílce. Ze vztahů (2) a (3) je patrné, že je užita geometricky přesná formulace modelu.
je pootočení i-tého dílce. Ze vztahů (2) a (3) je patrné, že je užita geometricky přesná formulace modelu.
3. Plocha potenciální energie
Popsaný model lze užít k mapování rozložení potenciální energie vzpěradla, ze které lze zjistit jak se bude vzpěradlo deformovat. Pro vykreslení energetické plochy do roviny byl použit postup prezentovaný v článku Frantík (2004.6), založený na hledání extrému potenciální energie Ep pomocí Newtonovy iterační metody:
1) Máme vzpěradlo v libovolném statickém stavu, nalezeném například pomocí Newtonovy iterační metody. Následně zafixujeme střední kloub vzpěradla.
2) Posuneme fixovaný střední kloub o „malý“ krok libovolným směrem a nalezneme opět extrém potenciální energie pomocí Newtonovy metody.
3) Bod dva opakujeme tak dlouho, dokud nedosáhneme bodu, v němž chceme znát hodnotu potenciální energie Ep. Zkontrolujeme dosažený stav a zaznamenáme hodnotu potenciální energie.
Tímto postupem byla získána energetická plocha znázorněná s pomocí transformace na obr. 5. Plocha je z praktických důvodů transformována do bezrozměrného tvaru tak, aby potenciální energie symetrické napjatosti (tj. kloub se posouvá pouze svisle; na obr. 5 svislá úsečka x = 0.6 m) měla hodnotu 1.00. Vrstevnice plochy byly získány z rastrové sítě vypočtených hodnot potenciální energie s pomocí programu Gnuplot, Williams et al. (2004).
Obr. 5 Transformovaná plocha potenciální energie vzpěradla, znázorněná pomocí vrstevnic, zobrazená v ploše možných poloh středního kloubu (libovolný bod v ploše představuje polohu středního kloubu vzpěradla, pro niž byl vypočten extrém potenciální energie)
Z obr. 5 je patrné, že nesymetrická napjatost, která je na obr. 5 patrná jako „kotlina“ při levém a pravém okraji zobrazené plochy, zřejmě představuje v případě zatěžování vzpěradla přírůstkem svislého posuvu w stabilní statický stav v celém intervalu existence této napjatosti (dle grafu na obr. 3). Symetrická napjatost, která je patrná jako svislá úsečka, je v tomto smyslu stabilním statickým stavem pouze v intervalu asi wstab  ( 0.48 , h ), tj. ystab
( 0.48 , h ), tj. ystab  ( 0 , 0.32 ), viz obr. 5. Ze zobrazené plochy je také vidět, že existuje další, dosud nepopsaný, nestabilní statický stav blízko souřadnic ( 0.37 , 0.35 ) a ( 0.83 , 0.35 ), patrný jako „lokální maximum“ vrstevnice 1.01, viz obr. 5. Tvar vzpěradla při dosažení tohoto stavu je zobrazen na obr. 6. Existence tohoto stavu indikuje, že na intervalu jeho výskytu jsou současně symetrická i nesymetrická napjatost stabilními statickými stavy.
( 0 , 0.32 ), viz obr. 5. Ze zobrazené plochy je také vidět, že existuje další, dosud nepopsaný, nestabilní statický stav blízko souřadnic ( 0.37 , 0.35 ) a ( 0.83 , 0.35 ), patrný jako „lokální maximum“ vrstevnice 1.01, viz obr. 5. Tvar vzpěradla při dosažení tohoto stavu je zobrazen na obr. 6. Existence tohoto stavu indikuje, že na intervalu jeho výskytu jsou současně symetrická i nesymetrická napjatost stabilními statickými stavy.
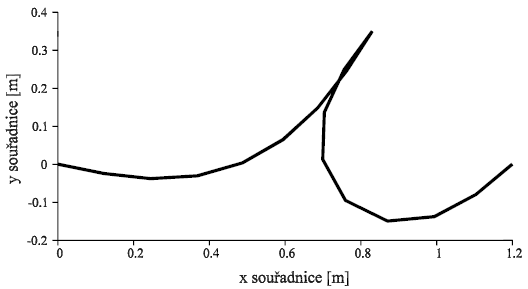
Obr. 6 Nalezený nový nestabilní statický stav s velmi omezenou oblastí výskytu
Dle plochy potenciální energie vzpěradla zobrazené na obr. 5 lze usoudit na následující průběh deformace vzpěradla h = 0.8 L: Máme-li vzpěradlo v počátečním nenapjatém stavu, pak „malý“ pokles středního kloubu způsobí zpočátku vybočení symetrickou napjatostí, která v důsledku libovolné nesymetrie počátečních podmínek přejde na nesymetrickou napjatost. Po dalším poklesu již bude vzpěradlo setrvávat v nesymetrické napjatosti až do okamžiku, kdy tato přestává existovat (tj. přibližně posuv w = 0.64 h, popř. bod y = 0.29 m). Po překročení tohoto kritického bodu nastává pád nesymetrické napjatosti na napjatost symetrickou, ve které vzpěradlo setrvá až do posuvu w = h, popř. do bodu y = 0.0 m.
4. Dynamické řešení
Pro ověření správnosti výše uvedené hypotézy o průběhu deformace vzpěradla byl formulován uvedený model jako nelineární dynamický systém. Pro jednoduchost je uvažováno, že se hmotnost prutu v modelu soustředí do „hmotných“ kloubů. Díky tomuto zjednodušení lze psát pohybové rovnice ve tvaru:
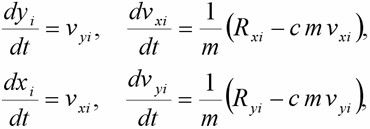 | (4) |
kde Rxi, Ryi jsou akce pružin na hmotné klouby, c je koeficient útlumu, m je hmotnost hmotných kloubů a vxi, vyi jsou rychlosti hmotných kloubů.
Ověření pomocí dynamického řešení bylo provedeno následujícím způsobem: V počátečním stavu byli vytvořeny dva pruty (složené z 8 dílců) ležící na ose x, spojené středním kloubem a na okrajích uložené na kloubových neposuvných podporách. Poté byl střední kloub zafixován proti pohybu ve svislém směru (nacházející se nyní na souřadnicích ( 1.0 , 0.0 ), viz souřadný systém na obr. 4. Následně se po malých krocích při probíhající simulaci posouvala pravá kloubová podpora z polohy x = 2.0 m do polohy x = 1.2 m, čímž vzniklo vzpěradlo v pokritickém tvaru. Poslední fází simulace bylo „pomalé“ posouvání středního kloubu (fixovaného ve svislém směru) vzhůru na souřadnici y = 0.8 m a zpátky dolů na souřadnici y = 0.0 m. Výsledek této simulace je zobrazen na obr. 7 v ploše potenciální energie vzpěradla.
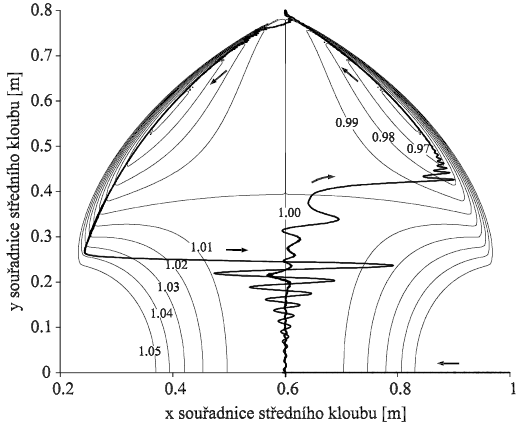
Obr. 7 Transformovaná plocha potenciální energie vzpěradla s vyznačením polohy středního kloubu v průběhu dynamické simulace (tučná křivka včetně směru pohybu)
5. Závěr
V článku bylo prezentováno ověření hypotézy o průběhu ztráty stability symetrického vzpěradla při pádu nesymetrické napjatosti pomocí dynamické simulace. Hypotéza byla simulací potvrzena, přičemž se ukázalo, že užitá metodika průzkumu plochy potenciální energie je zřejmě pro tyto účely dobře aplikovatelná a umožňuje vytvoření přehledného obrazu o vlastnostech jednoduchého nelineárního systému.
Poznamenejme, že pro podobné účely lze užít i analytického řešení pomocí teorie katastrof, viz Arnold et al. (1999), přičemž aplikace tohoto přístupu je předmětem budoucím.
Poděkování: Příspěvek byl vytvořen v rámci výzkumného centra CIDEAS (1M6840770001).
Literatura
Arnold V. I., Afrajmovich V. S., Il`Yashenko YU. S. & Shilnikov L. P. (1999) Bifurcation Theory and Catastrophe Theory. Springer-Verlag, New York.
Bažant Z. P. & Cedolin L. (1991) Stability of Structures. Oxford University Press, Oxford.
Frantík P. (2004.1) Rozbor existence řešení dokonalého symetrického vzpěradla. In: sborník mezinárodní konference Modelování v mechanice 2004, VŠB-TU Ostrava.
Frantík P. (2004.6) Stability Study of the Elastic Loop. In: proc. 5th International Ph.D. Symposium in Civil Engineering, vol. II, TU Delft, Netherlands.
Williams T., Kelley C. et al. (2004) GNUPLOT ver. 4.0. http://www.gnuplot.info/.