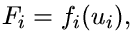
Abstrakt: V článku je popsán model s jedním stupňem volnosti, jenž může sloužit pro simulaci lomu trámce.
Numerická simulace porušení materiálu je při užití komplexních modelů výpočetně náročným problémem. Proto se pro rozsáhlejší úlohy a pro odhalování různých souvislostí může uplatnit model méně komplexní, prokáže-li se, že zjednodušení výrazně nesníží kvalitu dosažených výsledků. Z tohoto pohledu lze hledat co nejjednodušší systém, který bude mít odezvu podobnou odezvě komplexního modelu či výsledkům reálného experimentu.
Z experimentálních měření působení ohýbaných trámců z prostého betonu (se zářezem i bez zářezu) při zatěžování přírůstkem deformace lze získat zatěžovací diagram síla - průhyb i v případě, kdy se již trhlina šíří nestabilně - průhyb trámce vzrůstá a odpovídající zatěžující síla klesá, viz [1],[2],[7].
1 Úloha
Mějme trámec uložený a zatížený tak, aby u něj došlo k ohybovému porušení, například tzv. tříbodový ohyb, viz obr. 1. Předpokládejme, že je tento trámec vyroben z kvazikřehkého materiálu, jakým je beton. Při zatěžování trámce uděleným průhybem uprostřed rozpětí můžeme obdržet vzestupnou i sestupnou část zatěžovacího diagramu síla - průhyb, jak je vidět na obr. 2.
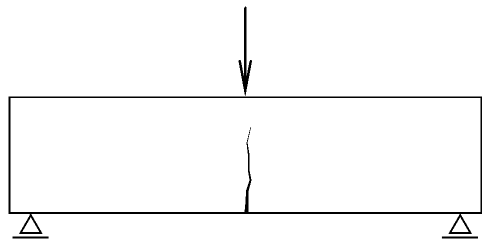
Obr. 1: Tříbodový ohyb trámce s ohybovým porušením
Na obrázku 2 je vidět typický diagram síla - průhyb pro tříbodový ohyb trámce z cementového kompozitu při porušení ohybem. Zatěžováním konstantním přírůstkem průhybu byla získána vzestupná i sestupná část diagramu.
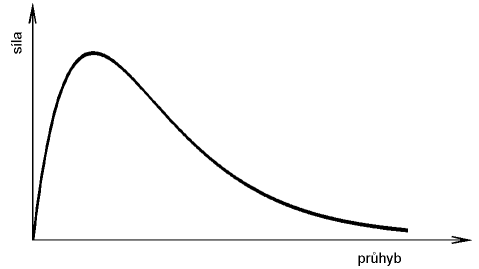
Obr. 2: Typická závislost síla - průhyb při ohybovém porušení
2 Model
Výstižné řešení popsané úlohy vyžaduje poměrně numericky náročné modely, jenž jsou vytvořeny zpravidla metodou konečných prvků s úpravami dle zásad lomové mechaniky (viz [5],[3]). Pokusme se nalézt méně komplexní model.
Zjednodušme výše popsanou úlohu zavedením symetrie a předpokládejme, že pro vystižení lomu trámce bude postačovat sledovat přetvoření vláken bezprostředně na ose symetrie (bližší úvahou je zřejmé, že tento předpoklad neplatí, což ale nemusí být na závadu). Jednu ze dvou symetrických polovin trámce nahradíme tuhou deskou připojenou k vetknutí kloubem a množinou vláken, která budou nahrazovat působící materiál, viz obr. 3.
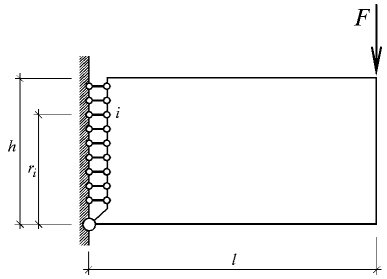
Obr. 3: Model trámce
Jelikož je tuhá deska připojena k vetknutí kloubem při jejím spodním okraji (viz obr. 3), není zohledněno působení materiálu v tlaku a navíc dochází též k zanedbání posunu neutrálné osy. Je prozatím otázkou jaký význam by mělo zahrnutí těchto součástí do modelu.
Samotné zatěžování trámce bude probíhat pootáčením desky okolo kloubu, jímž je připojena k vetknutí. Ze známého pootočení přímo vyplývá hledaný průhyb. Odpovídající zatěžující sílu lze stanovit z napjatosti vláken, reprezentujících materiál, u něhož je očekáváno porušení tahem. Dříve než přejdeme k vyjádření hledané závislosti síla - průhyb, je nutno definovat chování vláken v tahu.
Nechť ui je protažení i-tého vlákna vzdáleného od kloubu (středu otáčení desky) o hodnotu ri . Pak sílu Fi , kterou vlákno působí na desku, lze definovat vztahem:
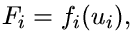| (1) |
kde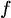 
i (ui ) je libovolná funkce napjatosti vlákna. Pro protažení i-tého vlákna, za předpokladu malých deformací, platí vztah (protažení vlákna je přímo úměrné jeho vzdálenosti od kloubu):
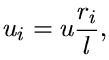 | (2) |
kde u je svislý posuv působiště zatěžující síly F, neboli průhyb trámce, a l je rameno zatěžující síly F (vzhledem ke kloubu), neboli polovina rozpětí trámce. Díky známému protažení každého vlákna a tedy známým silám, jimiž vlákna na desku působí, snadno stanovíme z momentové podmínky rovnováhy výslednou sílu F, odpovídající danému průhybu u:
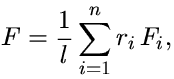 | (3) |
kde n je počet vláken. Tento vztah lze s užitím vztahů (1) a (2) přepsat:
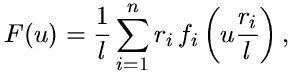 | (4) |
což je hledaná závislost síla - průhyb.
3 Tahové vlákno
Pro získání odezvy modelu popsaného v předchozí části potřebujeme definovat funkci napjatosti vlákna 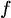i (ui ). Zvolme pro jednoduchost bilineární pracovní diagram, viz obr. 4. Funkce napjatosti 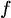i (ui ) pak může být definována:
 | (5) |
kde kincr,i je tuhost vlákna při pružném působení (což odpovídá sklonu vzestupné části diagramu), kdecr,i odpovídá sklonu sestupné části diagramu, upeak,i je protažení vlákna, při kterém je dosaženo maximální síly ve vláknu a uzero,i je maximální protažení vlákna (překročením této hodnoty dochází k jeho přetržení), viz obr. 4.
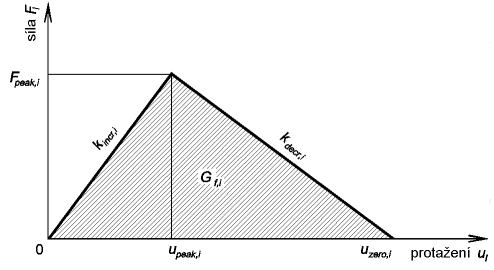
Obr. 4: Funkce napjatosti vlákna
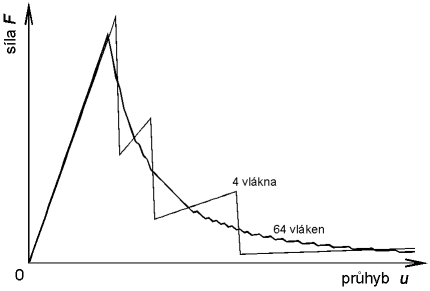
Funkce napjatosti bude pro každé vlákno definována parametry: tuhostí vlákna při pružném působení kincr,i , maximální tahovou silou Fpeak,i , kterou je vlákno schopno přenést (odpovídá tahové pevnosti vlákna) a specifickou lomovou energií vlákna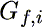 
, potřebnou pro jeho přetržení (tento přístup je v souladu s principy lomové mechaniky). Ostatní parametry, figurující v definici funkce napjatosti (5), je možné jednoznačně stanovit ze vztahů:
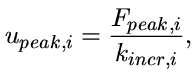 | (6) |
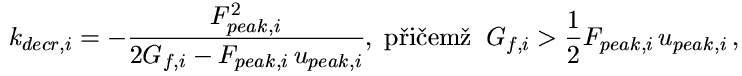 | (7) |
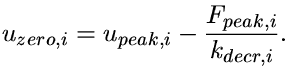 | (8) |
4 Aplikace
Budeme-li chtít popsat chování určitého trámce několika málo parametry takovými, které budou nezávislé na zvoleném počtu vláken ve výše popsaném modelu, je třeba najít vztahy, kterými lze vyjádřit souvislost těchto parametrů s parametry napjatostních funkcí vláken. Kromě polovičního rozpětí trámce l a výšky trámce h zvolme tři reprezentativní parametry: charakteristická tuhost v tahu trámce kt , charakteristická únosnost v tahu trámce ft a koeficient specifické lomové energie trámce ct . Pak lze parametry napjatostních funkcí jednotlivých vláken definovat takto:
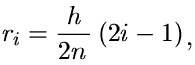 | (9) |
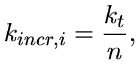 | (10) |
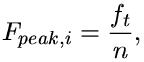 | (11) |
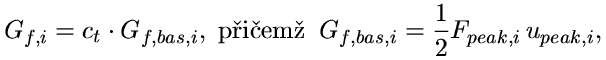 | (12) |
kde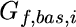 
vyjadřuje část specifické lomové energie, jež odpovídá natažení vlákna pro dosažení maximální tahové napjatosti. Koeficient specifické lomové energie trámce ct lze uvažovat z intervalu 
.
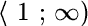Pro takto definované parametry lze ukázat, že odezva modelu velmi rychle konverguje se zvyšujícím se počtem vláken n. Rychlost konvergence závisí, z hlediska hladkosti získaného diagramu síla - průhyb, na koeficientu specifické lomové energie trámce ct , viz obr. 5 (srovnej s [6]). Čím bližší je koeficient ct dolní mezní hodnotě, tím méně hladká je odezva modelu (tato skutečnost jasně vyplývá z charakteru funkce napjatosti vlákna).
Obr. 5: Znázornění konvergence diagramu síla - průhyb modelu pro nejnepříznivější případ, tj. pro koeficient ct=1, který reprezentuje křehký materiál
Závěrem si ukažme jak se projeví hodnota specifické lomové energie na odezvě modelu. Na obr. 6 je vidět srovnání diagramů síla - průhyb pro různé hodnoty koeficientu specifické lomové energie ct .
Zvýšení hodnoty specifické lomové energie vláken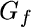 
se zřetejně projevilo změnou odezvy modelu. Za povšimnutí stojí známá skutečnost, že hodnota lomové energie má významný vliv na výslednou únosnost trámce v ohybu, viz [7].
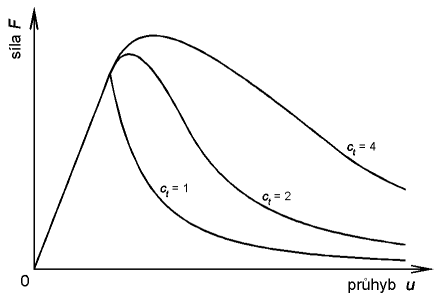
Obr. 6: Diagramy síla - průhyb modelu pro různé koeficienty specifické lomové energie vyjadřující křehkost materiálu
5 Závěr
V článku byl popsán jednoduchý jednostupňový model lomu trámce, inspirovaný výsledky zkoušek betonových trámců se zářezem ve tříbodovém ohybu s konstantním přírůstkem deformace.
Vzhledem k výstižnosti diagramů síla - průhyb získaných užitím modelu lze říci, že byl zřejmě podchycen hlavní mechanismus, jímž se transformuje chování materiálu v tahu na chování trámce v ohybu při ohybovém porušení. Model tak může sloužit pro hledání souvislostí mezi materiálovými charakteristikami či zkoumání vlivu variability parametrů úlohy.
Další možnou aplikací modelu je zkoumání lomu při ohybu trámců z jiných kompozitních materiálů, např. betonu s vlákny. Některé výsledky v tomto smyslu již byly prezentovány, viz [4].
Poděkování
Tento příspěvek byl vytvořen v rámci grantu GA ČR 103/03/1350, a s podporou výzkumného záměru MSM 261100009.
Literatura
[1] ALFAIATE, J., SIMONE, A., SLUYS, L. J. A new approach to strong embedded discontinuities. Computational modelling of concrete structures, Swets & Zeitlinger: Lisse 2003.
[2] BÍLEK, V., KERŠNER, Z., SCHMID, P., MOSLER, T. The toughness of concrete is not interesting for us, unless it loses it, International conference Non-traditional cement & concrete: Brno 2002.
[3] BRDEČKO, L. Některé aspekty řešení taženého prutu plynoucí z uvažování tahového změkčení. Seminář Problémy lomové mechaniky III.: Brno 2003.
[4] FRANTÍk, P. L-d diagramy se dvěma vrcholy II. - jednoduchý model, XXVI. komorní seminář Úskalí lomové mechaniky kompozitů na silikátové i jiné bázi, http://www.fce.vutbr.cz/stm/fracture/kseminar/ks26/zprava.htm, VUT FAST v Brně: Brno 2004.
[5] PATZÁK, B., JIRÁSEK, M. Adaptive simulation of quasibrittle fracture. Computational modelling of concrete structures, Swets & Zeitlinger: Lisse 2003.
[6] PAZ, C.N.M., MARTHA, F.F., ALVES, J.L.D., EBECKEN N.F.F., FAIRBAIRN, E.M.R, COUTINHO, A.L.G.A. A computational approach for three-dimensional probabilistic discrete cracking in concrete. Computational modelling of concrete structures, Swets & Zeitlinger: Lisse 2003.
[7] ŘOUTIL, L., LEHKÝ , D. Tříbodový ohyb trámce se zářezem, Statistická a citlivostní analýza Atena/Freet. Seminář Problémy lomové mechaniky III.: Brno 2003.