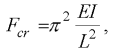
ABSTRACT: Research of stability of the elastic loop is presented. The loop is produced by the solving of the ideal slender beam buckling problem. The special discrete nonlinear model of the beam is used. In order to find a solution of this model the Newton iterative method is used. The loop stability is confirmed by investigation of the model potential energy distribution.
Keywords: elastic beam buckling, potential energy, system stability, large displacements
1 INTRODUCTION
Beam buckling problem is in our focus: The simple supported beam of linear elastic material loaded by force F, see Figure 1. An ideal very slender prismatic beam with the length L and with the bending stiffness EI is considered.
The shear strain and constant component of the normal strain can be neglected due to the beam slenderness.
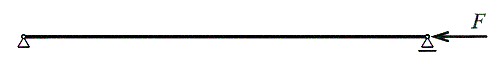
Figure 1. The beam buckling problem: The precritical state.
Exact precritical solution of this problem is known (Euler 1744) and gives to us the critical value of the force F,
for the loss of the stability of the straight shape of the beam:
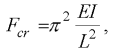| (1) |
where Fcr is the critical value of the force F.
Exact postcritical solution of this problem with respect to the large displacements is also known (Rzanicin 1955)
and gives a wide scale of shapes, see Figure 2. There is a possibility of the occurrence of the loop (last shape
in Figure 2).
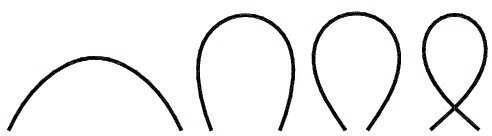
Figure 2. The beam buckling problem: the postcritical deformed shapes of the beam.
2 PROBLEM
Postcritical solution of the beam buckling can be found by simulation of the dynamic system, which represent the tested beam and load. The advantages of this approach are location of the stable solutions only, location of the ways of the loss of stability and simple controlling of the system evolution. The disadvantages of this approach are impossibility of location of the general unstable solutions (some unstable solution can be found - for example the straight shape of the beam with postcritical load), complications with definition of the dynamic model and time-cost of the dynamic simulation.
The described dynamic approach and some interesting results were presented in the paper Frantík 2002. It was observed, that postcritical solution, according to exact postcritical solution (Rzanicin 1955), see above, is perhaps not stable for the value of the force F greater than a specific value. For these values of the force F the beam shape is the loop (see the last shape in Figure 2). The next observed fact was the possibility of the two different ways of the loop downfall, see Figure 3.
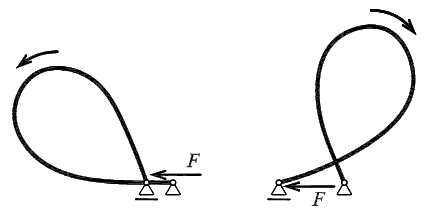
Figure 3. The visualisation of the two ways of the loop downfall.
This paper is just focused on the establishment of the loop stability. The special static model for determination of the potential energy distribution in the loop surroundings will be used here.
3 DISCRETE MODEL
Let us consider similar conditions like in the first section, but we do not neglect the constant component of the normal strain. According to this condition, it is necessary to add one new parameter - the normal stiffness of the beam EA.
The special discretization method was used to find the beam shapes and determination of the potential energy of the beam. The beam is divided into a number of the same straight linear elastic physical segments connected by hinges with the same linear elastic rotational springs, see Figure 4.
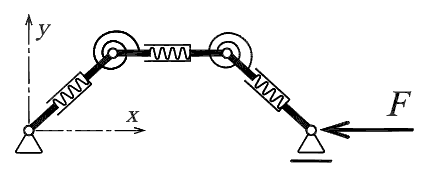
Figure 4. The discrete model of the beam with three segments.
The internal force N acts in every elastic segment. The force N is directly proportional to the difference dl between the original length of the segment l and the actual length l+dl:
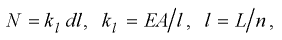 | (2) |
where kl is the stiffness of elastic segment and n is the number of segments.
Every rotational spring acts by the bending moment M on the connected segments, which is directly proportional to the difference d 
between them:
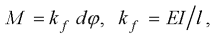 | (3) |
where kf is the stiffness of the rotational spring.
Then the potential energy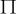 
of the discrete system (beam with load) can be described by relationship:
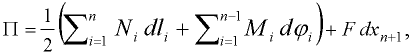 | (4) |
where dxn+1 is the horizontal displacement (x direction) of the sliding support (see Figure 4).
We can use relations (2), (3) and change relation (4) into:
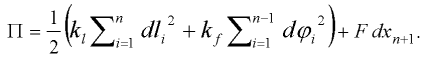 | (5) |
State of the system is fully given by coordinates (x, y) of every hinge. Therefore we need to know the dependency of the system potential energy 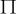on this coordinates. According to the geometry of the model we can write:
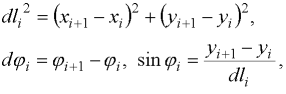 | (6) |
where (xi, yi) are Cartesian coordinates of the hinge (alias supports, see Figure 4) with the index i for which apply
i = 1, 2, …, n +1.
4 SOLUTION
If we have the relationship for the potential energy of the system (relations (5) and (6)), we can differentiate this relationship and obtain a system of nonlinear algebraic equations. Then the equation system can be solved by some iterative method, e.g. the Newton method.
Here was successfully used the Newton iterative method with the numeric differentiation of the system potential energy .
Following method was used for the searching of the potential energy distribution of the energetic surroundings of the loop (it is problem of projection in the 2n+2 dimensional space):
for this point.We can map the energetic surroundings of a solution by the described method. Figure 5 shows the selected loop for the force F = 2Fcr (the length of the beam L = 1 m, the bending stiffness EI = 1 Nm2, the normal stiffness
EA = 100 N, the critical force Fcr = 11 N, and model with n = 10 segments).
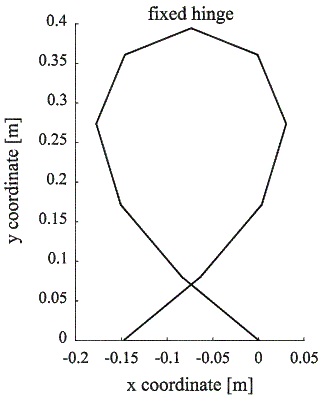
Figure 5. The loop F = 2Fcr with the signed fixed middle hinge.
The potential energy distribution in the surroundings of the same loop is shown in contour representation in Figure 6. We can see the area of the possible positions of the fixed hinge near the saddle point, which represents the investigated solution - loop. Therefore the loop for the force F = 2Fcr is not a stable solution. The motion in x direction gives the ways of the loop fall: to the left (-) and to the right (+), (see Figure 3).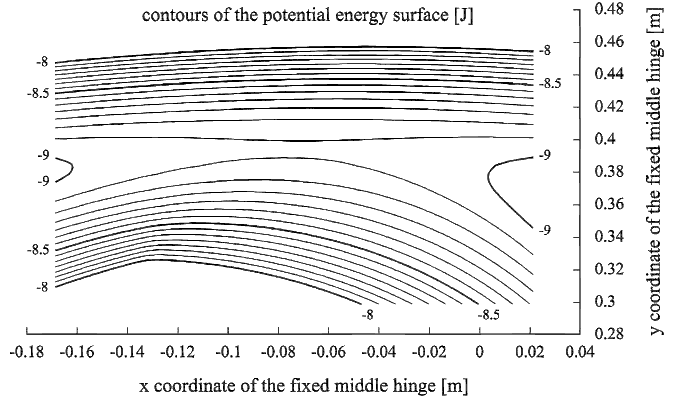
Figure 6. Representation of the potential energy distribution in the surroundings of the loop.
We can investigate the energetic situation of the beam buckling solution with the change of the postcritical value of the force F. It is needed for searching of the moment of loss of solution stability. It was discovered that it is possible to observe only the changes of energetic situation in x direction nearby the solution. 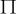We can select one point nearby the solution and compare its potential energy near with the potential energy of the solution sol.
We can define the curvature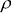 
x in x direction for good comparability:
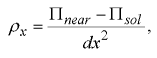 | (7) |
where dx is the small displacement of the fixed middle hinge in x direction from the point, which represents the middle hinge of the solution. The curvature 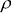x reflects the energetic situation (positive value - stable, negative value - unstable). In Figure 7 is shown a graph of the curvature 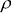x depending on the value of the force F
(in dimensionless form). We can see, that the solution is stable only in interval (Fcr , 1.74 Fcr). Point F = 1.74 Fcr means the contact between the supports of the beam - the loop occurrence.
Figure 7. Dependency between the energetic surface curvature 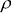x and the force F.
5 CONCLUSIONS
The stability of the solution of the ideal beam buckling problem was confirmed in the paper. The special static nonlinear discrete model was used to find the solution and for determination of the potential energy of any deformed beam shape.
The projection of many-dimensional space into three-dimensional space was successfully used. The methodology can be applied in an arbitrary other complicated nonlinear problem (problems with multiple solutions).
It was proved, that the solution of the beam buckling problem is not stable, if the solution generates the loop. This conclusion can have wide impact, because a similar loop can occur by different systems, e.g. the bending of the elastic slender cantilever beam (Frantík 2003).
ACKNOWLEDGEMENT
The research is provided under Czech research project CEZ: J 22/98: 261100009 and supported by grant No. 103/04/2092 from the Grant Agency of the Czech Republic
REFERENCES
Euler, L. 1744. Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes. Marcum Michaelem Bosquet, Lausanne.
Rzanicin, A.R. 1955. Ustojcivost ravnovesia uprugich sistem. Gosudarstvennoje izdatelstvo techniko-teoreticeskoj literatury, Moskow.
Frantík, P. 2002. Instabilities of the Selected Systems. International Conference Engineering Mechanics 2002: CD-ROM. Svratka, Czech Republic.
Frantík, P. 2003. Nonlinear Solution of Cantilever Beam Deflection II. 5. International Phd Conference, CD-ROM. Brno, Czech Republic: Faculty of Civil Engineering, Brno University of Technology.