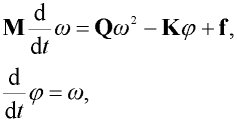
Summary: Postcritical free vibrations of a slender elastic beam are studied. Cantilever beam is loaded by axial force and lateral deflections are observed. Effective numerical model of the beam is used and described. Vibration properties are investigated by Fourier frequency analysis.
1. Úvod
Ideální štíhlý prut z pružného materiálu, zatížený ve vzpěru dostatečně velkým zatížením, může dosáhnout kritického stavu, který je již dlouho dobře znám. Překročí-li zatížení velikost nutnou pro tento kritický stav, dochází ke ztrátě stability přímého tvaru prutu při bifurkaci do jednoho ze dvou symetrických stabilních stavů (v rovinném případě). Tato úloha, i ve své statické podobě, je z hlediska výpočetní náročnosti poměrně složitá. Navíc je známo, že v okolí bifurkačního bodu se každý numerický model prutu chová do určité míry nestabilně. Hledání řešení takového prutu v pokritickém stavu dává zajímavé výsledky, jak je patrné například z publikace (Frantík 2004). Zde se věnujme vlastnostem volného kmitání prutu v pokritickém stavu se zaměřením na frekvenční analýzu pomocí Fourierovy transformace.
2. Model prutu
Pro výpočet kmitání štíhlého konzolového prutu byl vytvořen speciální model (viz Frantík & Macur, 2003), který umožňuje efektivní řešení zvolené úlohy. Je uvažován velmi štíhlý prut konstantního průřezu z lineárně pružného materiálu, což umožňuje zanedbat práci normálových i posouvajících sil na přetvoření prutu. Prut je ekvidistantně rozdělen na tuhé dílce spojené klouby s lineárními rotačními pružinami, viz obr. 1. Tento model lze dle (Henrych 1985) zařadit mezi finitní metody mechaniky jako zvláštní případ metody fyzických konečných prvků.
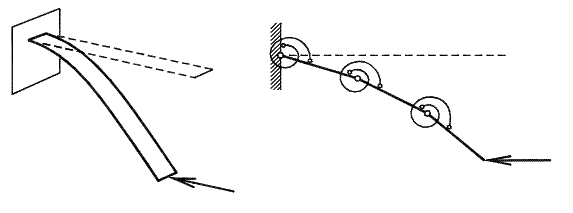
Obr. 1: Znázornění řešené konstrukce a jejího modelu
Konzervativní pohybové rovnice modelu (nejsou uvažovány tlumící jevy), odvozené v (Frantík & Macur 2003), lze zapsat v maticovém tvaru:
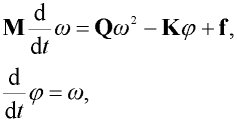| (1) |
kde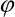 
je vektor pootočení dílců, 
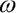je vektor úhlových rychlostí dílců, M je plná symetrická matice momentů setrvačnosti dílců, Q je podobná antimetrická matice, K je třídiagonální matice tuhosti, f je vektor momentů zatěžující síly (působící na konci prutu ve směru jeho nepřetvořené osy) a t je čas. Matice momentů setrvačnosti M má tvar:
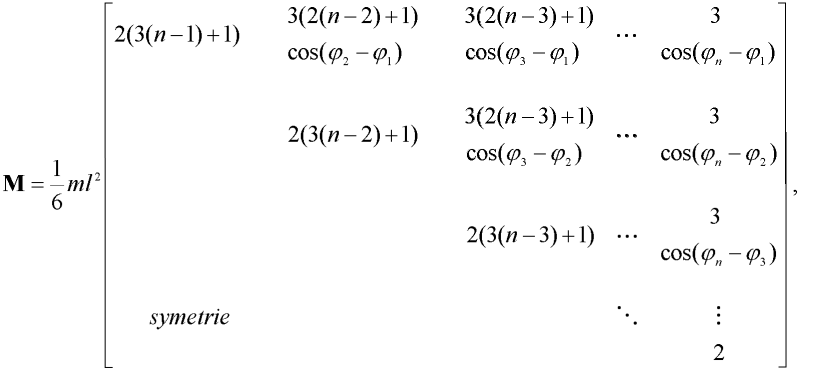 | (2) |
kde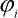 
je pootočení i-tého dílce, vzato vzestupně od dílce u vetknutí prutu, n je počet dílců, l je délka dílce a m je hmotnost dílce. Dále pro matici Q platí:
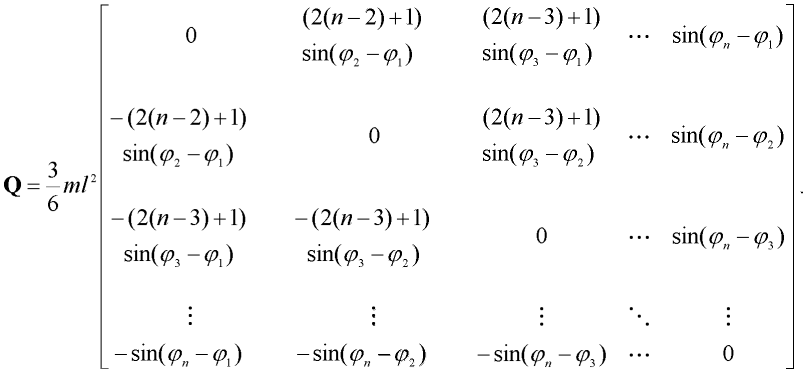 | (3) |
Jestliže k je tuhost rotačních pružin, pro kterou platí k = EI/l, kde EI je ohybová tuhost prutu, pak pro matici tuhosti K platí:
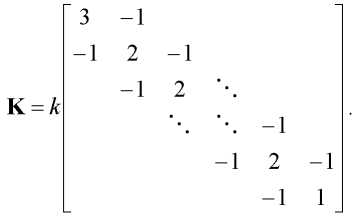 | (4) |
Pro vektor momentů zatěžující síly f platí:
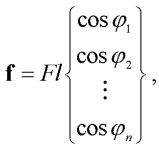 | (5) |
kde F je síla působící na konci prutu ve směru jeho nepřetvořené osy.
Řešení pohybových rovnic (1) lze vzhledem k jejich nelinearitě provést s pomocí diferenčních explicitních numerických metod pro řešení počátečního problému obyčejných diferenciální rovnic. Jistou komplikací je v tomto případě plná matice momentů setrvačnosti M, protože je tímto nutné v každém kroku diferenční metody řešit minimálně jednou soustavu lineárních algebraických rovnic. Tento nedostatek je plně kompenzován (co do časové náročnosti modelu) zanedbáním práce normálových a posouvajících sil. Díky tomuto zanedbání jsou maximální dosahované frekvence při řešení až o dva řády nižší (v závislosti na štíhlosti prutu), což umožňuje velmi rychlé simulace.
3. Volné kmitání
S pomocí modelu popsaného v předchozí části můžeme řešit libovolná posunutí prutu, jelikož je v něm plně uvažována geometrická nelinearita úlohy (za předpokladu rozdělení prutu na dostatečný počet dílců při velkých rotacích dílců). Tento model užijeme pro výpočet volného kmitání prutu zatíženého ve vzpěru, jak bylo naznačeno v úvodu. Počátečním stavem bude nepřetvořený prut zatížený silou F na jeho konci a každý dílec bude mít udělenu velmi malou počáteční úhlovou rychlost 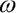. Tento výpočet proveďme pro různé hodnoty síly F a sledujme vývoj amplitudového spektra Fourierovy transformace časové řady příčné výchylky koncového bodu prutu.
Výpočtem můžeme zjistit, že je-li síla F nižší než kritická hodnota Fcr, pro kterou platí známý vztah odvozený Eulerem Fcr =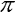 
2EI / 4lc2, kde lc je délka prutu, pak obdržíme jen jedinou dominantní frekvenci (viz obrázek 2). Volné kmitání v prekritickém stavu prutu při malých deformacích lze totiž považovat za harmonické (je to dáno linearitou problému). Pro tuto dominantní frekvenci 
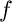precr platí přibližně vztah (srovnej s obr. 4):
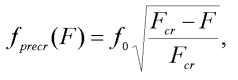 | (6) |
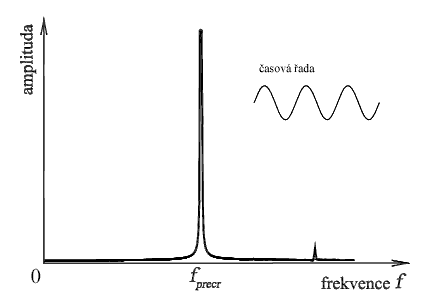
Obr. 2: Amplitudové spektrum volného kmitání prutu v prekritickém stavu
kde 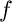0 je nejnižší frekvence volného kmitání nezatíženého prutu, pro kterou přibližně platí, dle (Brepta a kol. 1994):
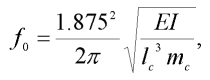 | (7) |
kde mc je hmotnost prutu.
Pro sílu F větší než je kritická hodnota Fcr (pokritický stav) je výsledek Fourierovy transformace složitější, jelikož je úloha již výrazně nelineární a výsledná časová řada příčné výchylky nemá harmonický průběh (viz obr. 3).
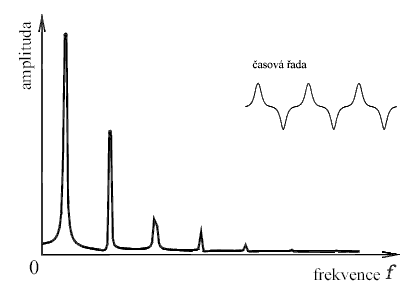
Obr. 3: Amplitudové spektrum volného kmitání prutu v pokritickém stavu
Plošné zobrazení vývoje amplitudového spektra při změně velikosti síly F je vidět na obr. 4 včetně grafu vrcholů amplitud (velikost amplitudy je v plošném zobrazení dána odstínem šedé - čím tmavší, tím větší amplituda).
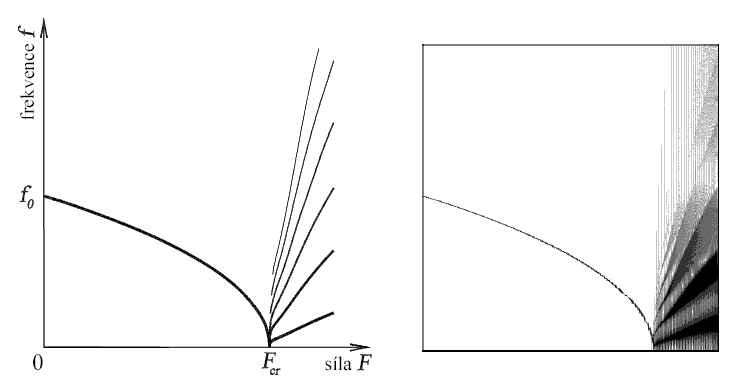
Obr. 4: Graf dominantních frekvencí (vrcholů amplitud Fourierovy transformace - vlevo) a původní výsledné amplitudové spektrum Fourierovy transformace časové řady příčné výchylky (vpravo) v plošném zobrazení.
4. Aproximace
Z podrobnější analýzy průběhu amplitudového spektra pokritického kmitání vyplývá, že vzájemný odstup sousedních dominantních frekvencí je přibližně konstantní, přičemž první dominantní frekvence je polovinou tohoto odstupu, dále amplitudy pro tyto dominantní frekvence přibližně exponenciálně klesají a fáze následující dominantní frekvence je vždy posunuta o 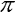rad. Časovou řadu příčné výchylky tedy bude zřejmě možné aproximovat řadou:
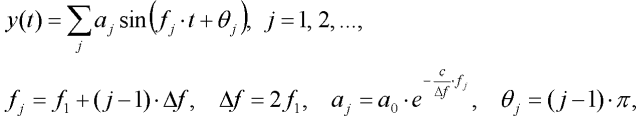 | (8) |
kde y je příčná výchylka koncového bodu prutu, 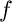1 je první dominantní frekvence, a0 je charakteristická amplituda a c je koeficient strmosti poklesu amplitud. Tato řada může dát velmi dobré výsledky, jak je patrné ze srovnání vybrané časové řady při pokritickém kmitání a její aproximace na obrázku 5.
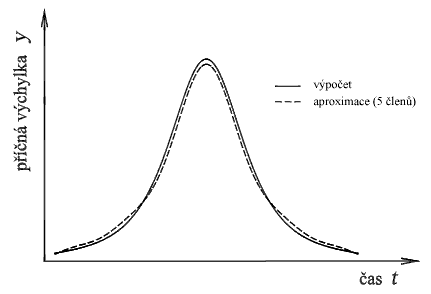
Obr. 5: Srovnání vypočtené a aproximované půlvlny příčné výchylky. Pro aproximaci bylo užito 5 členů řady
5. Závěr
V příspěvku byly ukázány zjištěné vlastnosti volného kmitání vetknutého prutu, který je v pokritickém stavu. Ukázalo se, že frekvenční spektrum příčné výchylky koncového bodu prutu má jedinečné vlastnosti (při zvolených počátečních podmínkách) a lze snadno aproximovat pomocí harmonické řady s exponenciálním poklesem amplitud.
Volné kmitání prutu v pokritickém stavu bylo řešeno s pomocí speciálního modelu, který byl v článku detailně popsán. Tento model se ukazuje být efektivní při rozsáhlých výpočtech silně nelineárních úloh tohoto druhu.
Poděkování
Tento příspěvek byl vytvořen v rámci výzkumného záměru CEZ: J22/98: 261100009 a s podporou grantu GA ČR 103/03/1350.
Literatura
Brepta R., Půst L., Turek F. (1994), Mechanické kmitání, Technický průvodce 71, nakladatelství Sobotáles, Praha
Frantík, P. (2004) Stability study of the Elastic Loop, 5th International PhD Symposium in Civil Engineering, TU Delft, Netherlands
Frantík, P., Macur, J. (2003) Diskrétní dynamický model konzoly: Speciální řešení, konference DYN-WIND, TU Žilina, Tále
Henrych J. (1985) Úplná soustava finitních metod mechaniky a možnosti dalšího rozvoje, studie ČSAV 6.85, nakladatelství Akademia, Praha