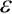(dle [4]):
ÚVOD
Lze říci, že problematika geometricky nelineárních řešení pružných prutových konstrukcí je v současnosti velmi dobře vyřešena. Je možno hledat téměř libovolné deformace (posunutí) prutů v dobrém souladu se skutečností. Nicméně souvislosti užitých předpokladů si možná právě proto zasluhují (vzhledem ke snaze pochopit jejich význam) bližší zkoumání.
Tento příspěvek se zabývá hledáním průhybu štíhlého konzolového nosníku zatíženého vertikálním gravitačním polem (viz obr. 1) v oblasti velmi velkých deformací a volně tak navazuje na předchozí dva články [1] a [2], které se zabývaly problematikou hledání řešení průhybu konzolového nosníku zatíženého silou, publikované v minulých ročnících téže konference. Současně však tento příspěvek přímo souvisí s článkem [3], kde byl publikován obdobný případ s odlišnou (horizontální) orientací gravitačního pole.
1 ÚLOHA
Mějme štíhlý konzolový nosník konstantního průřezu v gravitačním poli působícím ve směru kolmém na osu nepřetvořeného prutu, viz obrázek 1. Předpokládejme ideálně přímý nosník natolik štíhlý, že se jeho materiál chová lineárně pružně pro libovolné posunutí (pro dané konečné posunutí je tato úloha reálná).
Obr. 1 Konzolový nosník v gravitačním poli
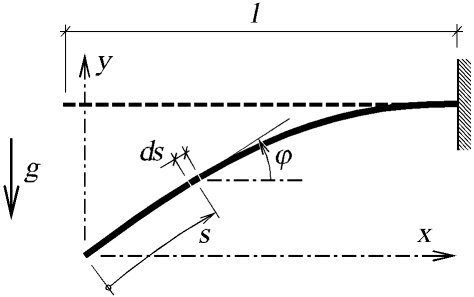
Hledejme obecné řešení posunutí prutu s užitím předpokladu zachování rovinnosti průřezu po deformaci a zachování jeho kolmosti ke střednici (není uvažována práce posouvajících sil). Vzhledem k velké štíhlosti prutu zanedbejme také práci normálových sil. Za těchto předpokladů můžeme pro průřez se souřadnicí s měřenou po střednici prutu (viz obr. 2) psát vztah pro normálové poměrné přetvoření 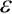(dle [4]):
 | (1) |
kde 
(s) je funkce pootočení průřezu a z je souřadnice vlákna průřezu měřená kolmo od střednice prutu v rovině ohybu. Tento vztah je za daných předpokladů přesný a umožňuje přesně řešit libovolná posunutí prutu.
Obr. 2 Konstrukce včetně označení
2 APROXIMACE
Uvedené předpoklady sice umožňují nalézt přesné řešení této úlohy, nicméně je to stále příliš složitá úloha. Abychom ji zjednodušili, uvažujme, že (za daných předpokladů) je přesná funkce pootočení průřezu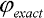 
(s) blízká svým tvarem funkci:
 | (2) |
kde a je hledaný neznámý parametr a l je délka nosníku. Tato funkce odpovídá svým tvarem lineárnímu řešení této úlohy. Lze snadno ukázat, že pro malá posunutí platí vztah s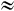 
x, kde x je souřadnice průřezu prutu měřená ve směru osy nepřetvořeného prutu. Dosazením do výrazu (1) dostáváme známý vztah:
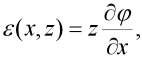 | (3) |
jehož aplikací na zvolenou úlohu (a užitím dalších, obecně užívaných, přípustných zjednodušení v teorii malých deformací: tan 
, cos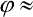 
1, sin ) můžeme získat:
 | (4) |
kde A je plocha průřezu prutu,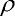 
je hustota (popř. objemová hmotnost) materiálu prutu a g je tíhové zrychlení. Toto lineární řešení (4) lze nazvat tečným řešením k přesnému řešení pro zatížení A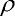g = 0 a lze proto očekávat, že obdobná funkce (2) je dobrou výchozí podmínkou pro nalezení dalšího stupně aproximace přesného řešení.
3 ŘEŠENÍ
Nyní již máme zvoleno vše, co je třeba k vyřešení úlohy. Víme, jaké poměrné přetvoření vzniká vlivem natočení průřezů (vztah (1)) a máme zvolenu aproximační funkci pootočení průřezů (2) s jedním neznámým parametrem a. Abychom stanovili jeho hodnotu, užijeme s výhodou Ritzovu metodu s uplatněním principu minima potenciální energie systému. Víme, že pro potenciální energii systému (konstrukce + zatížení) 
platí:
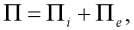 | (5) |
kde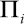 
je potenciální energie deformace konstrukce (energie akumulovaná v prutu vlivem jeho pružného přetvoření) a 
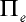je potenciální energie zatížení (hmota prutu pohybující se v gravitačním poli).
3.1 Potenciální energie deformace prutu
Odvod'me nejprve výraz pro energii akumulovanou v prutu. Jelikož uvažujeme fyzikálně lineární materiál (Hookeův zákon), tak pro potenciální energii deformace prutu 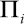platí:
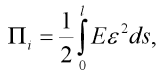 | (6) |
kde E je modul pružnosti materiálu prutu. Užitím vztahu (1), úpravou (substitucí momentu setrvačnosti průřezu I) a vytknutím konstant, lze tento vztah upravit na:
 | (7) |
kde součin EI je ohybová tuhost průřezu prutu. Dosadíme-li do tohoto vztahu zvolenou aproximaci funkce pootočení , výraz (2), tak po integraci můžeme obdržet vztah:
 | (8) |
3.2 Potenciální energie zatížení
Sestavení energetické bilance zatížení je trochu obtížnější. Je zřejmé, že vlivem posunutí prutu se mění poloha jeho hmoty. Protože je prut umístěn v gravitačním poli, tak dochází ke změně potenciální energie této hmoty (hmota v gravitačním poli klesá). Lze říci, že každý myšlený hmotný element ds prutu ztrácí pohybem v gravitačním poli g potenciální energii 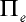úměrnou své hmotnosti dm (pro kterou platí dm = A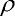ds), intenzitě gravitačního pole g a posunu v ve směru gravitačního pole. Platí:
 | (9) |
což lze pro celý prut přepsat (provedeme integraci a vytkneme konstanty):
 | (10) |
přičemž v(s) je funkce posunutí hmotného elementu prutu A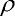ds (se souřadnicí s) ve směru gravitačního pole (tj. ve směru kolmém na osu nepřetvořeného prutu). Z geometrických souvislostí plyne (viz obr. 2), že je možné funkci posunutí v(s) vyjádřit s pomocí funkce souřadnice průřezu y(s) ve tvaru (počátek souřadného systému je umístěn netradičně na volném konci konzoly):
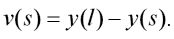 | (11) |
Dále pro funkci souřadnice průřezu x(s) (připomeňme, že je měřena ve směru osy nepřetvořeného prutu) platí:
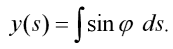 | (12) |
Řešení tohoto integrálu je zřejmě obtížné. Řešme jej tedy pouze přibližně s užitím prvních dvou členů Taylorova rozvoje funkce sin x. Můžeme psát:
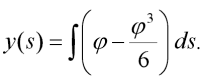 | (13) |
Tento integrál lze již snadno s užitím aproximační funkce (2) vyřešit (obsahuje pouze polynom vysokého stupně) a tak obdržet vztah:
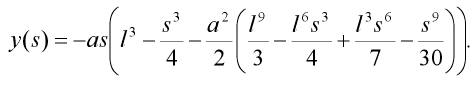 | (14) |
Dosazením délky prutu l za souřadnici s do odvozeného vztahu (14) pro souřadnici y dostaneme:
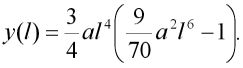 | (15) |
což je výraz pro souřadnici y vetknutého konce prutu a zároveň příčné posunutí volného konce konzoly. Nyní máme k dispozici vše potřebné pro sestavení potenciální energie zatížení 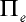. Dosad'me nalezené přibližné výrazy (14) a (15) do vztahu pro posunutí v (11) a tento pak do integrálu potenciální energie zatížení 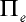(10) a proved'me integraci. Můžeme tak obdržet (vzhledem k nahrazení funkce sin x v integrálu (12) pouze přibližně):
 | (16) |
čímž jsme zakončili stanovení dílčích energetických bilancí.
3.3 Řešení
Díky úspěšnému sestavení dílčích složek (tj. potenciální energie deformace 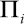a potenciální energie zatížení 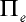) můžeme nyní, s užitím vztahů (5), (8) a (16), psát pro celkovou potenciální energii systému :
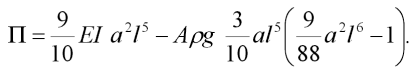 | (17) |
Víme, že pro stabilní řešení úlohy musí potenciální energie systému nabývat lokálního minima (jakákoliv změna vyžaduje přidanou energii) a tedy musí být v našem případě alespoň splněna podmínka (hledáme parametr a):
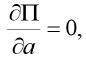 | (18) |
což dává, po dosazení vztahu (17), provedené derivaci a úpravě, kvadratickou rovnici:
 | (19) |
která má dvě řešení:
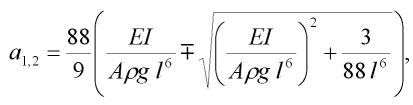 | (20) |
přičemž řešení a1 je hledaným prvním stabilním řešením úlohy a řešení a1 je přiblížení k prvnímu nestabilnímu řešení úlohy (obdobně jako v případě řešení [1]).
Pro doplnění odvoďme vztah pro souřadnici x(s) průřezu s deformovaného nosníku. Postupujme stejně jako v případě souřadnice y. Víme, že platí::
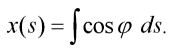 | (21) |
Tento integrál řešme přibližně s užitím dvou členů Taylorova rozvoje funkce cos x:
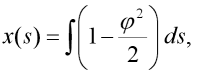 | (22) |
s pomocí kterého lze po dosazení aproximační funkce (2), integrací a úpravou obdržet:
 | (23) |
Dosazením délky prutu l za souřadnici s do vztahu (23) dostaneme přibližný výraz pro horizontální souřadnici vetknutého konce konzoly:
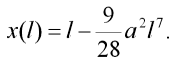 | (24) |
4 SROVNÁNÍ
Srovnejme nalezené řešení s přesnějším řešením. Přesnější řešení je možno obdržet například aplikací diskrétní metody tuhých dílců, kterou lze, dle soustavy finitních metod mechaniky [5], považovat za speciální případ metody tuhých fyzických konečných prvků. Na obr. 3 je vidět graf (v bezrozměrném tvaru) srovnání nalezeného řešení s řešením lineárním a řešením metodou tuhých dílců, které lze při daném zobrazení považovat za přesné.
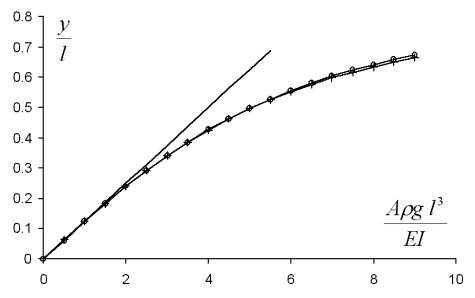
Obr. 3 Graf svislého posunu volného konce nosníku
ZÁVĚR
Odvozené geometricky nelineární řešení průhybu konzolového nosníku zatíženého tíhovým polem ukázalo výstižnost vybrané aproximace (chyba menší než 2% pro svislý posun volného konce y = 0.7l) a také platnost užitého vztahu pro poměrné přetvoření. Význam tohoto řešení je možno vidět zejména při kontrolních výpočtech, v pedagogické oblasti, kdy se zájem soustředí na pochopení souvislostí při geometricky nelineárních problémech a případně v praxi, kdy je potřeba přesněji odhadnout průhyb při velkých deformacích bez použití výkonné výpočetní techniky.
Poděkování
Tento příspěvek byl vytvořen v rámci výzkumného záměru CEZ: J22/98: 261100009, s podporou grantu GA ČR 103/03/1350 a nadace Preciosa.
LITERATURA
[1] FRANTÍK, P. Nelineární řešení průhybu konzoly, 4. odborná konference doktorského studia, VUT FAST v Brně, Brno, únor 2002, ISBN 80-214-2067-7.
[2] FRANTÍK, P. Nelineární řešení průhybu konzoly II, 5. odborná konference doktorského studia, VUT FAST v Brně, Brno, únor 2003, ISBN 80-7204-265-3.
[3] FRANTÍK, P. Spojitá aproximace prutu při ztrátě stability od vlastní tíhy, vědecký seminář Modelování v mechanice 2004, VŠB-TU Ostrava, leden 2004.
[4] RŽANICIN, A. R. Ustojčivost' ravnovesija uprugich sistem, Gosudarstvennoje izdatel'stvo techniko-teoretičeskoj literatury, Moskva, 1955.
[5] HENRYCH, J. Úplná soustava finitních metod mechaniky a možnosti dalšího rozvoje, studie ČSAV 6.85, nakladatelství Akademia, Praha, 1985.