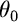, které figuruje v tomto řešení jako parametr, jenž měníme v průběhu iterace. Je-li zvoleno 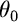, pak stačí vyřešit postupně následující dílčí výrazy (převzato z [3]):
Abstract
The analysis of the postcritical solutions of the von Mises truss is described in the paper. There is single parameter study of the order and existence of the symmetric and antimetric stress.
Úvod
Zde prezentované výsledky navazují na články [1] a [2] publikované na minulém ročníku téže konference. Zmiňované články se zabývají nalezenými přibližnými analytickými řešeními pokritického působení symetrického vzpěradla (viz obrázek 1) a to jak symetrickou napjatostí [1] tak nesymetrickou napjatostí [2]. Ukázalo se, že obecné vzpěradlo nabízí rozmanité pokritické chování, které si zaslouží hlubší zkoumání. Tento příspěvek se zabývá jednoparametrickou studií vzpěradla právě vzhledem k existenci jeho pokritických řešení.
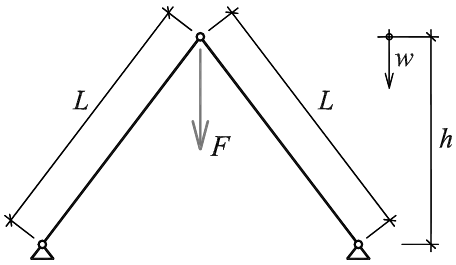
Figure 1: Vzpěradlo
1 Vzpěradlo
Uvažované vzpěradlo je jednoduchá, symetrická, staticky určitá prutová konstrukce, znázorněná i s uvažovaným zatížením na obrázku 1. Necht' se skládá ze dvou stejných ideálně přímých štíhlých prutů konstantního průřezu z fyzikálně lineárního materiálu.
Uvažujme, že ke změně tvaru vzpěradla dojde jedině tehdy, jestliže alespoň jeden prut vybočí. Tento požadavek znamená zanedbání normálového a smykového přetvoření prutů vzpěradla. Pro definici vzpěradla tak vystačíme se třemi nezávislými parametry: délkou prutů L, výškou vzpěradla h a ohybovou tuhostí prutů EI, přičemž jako proměnlivý parametr budeme uvažovat výšku vzpěradla h.
Požadované řešení vzpěradla, daného trojicí parametrů, pak bude hledání závislé dvojice zatížení-posunutí, přičemž zatížením je svislá síla F působící ve středním kloubu vzpěradla a posunutím je svislý posun w středního kloubu vzpěradla.
Protože pro řešení této úlohy požadujeme vybočení prutu, je nezbytné, abychom správně vystihli chování prutu ve vzpěru.
2 Vzpěr prutu
Samotná úloha vzpěru ideálního prutu je potřebnou klíčovou znalostí při pokritickém řešení štíhlého vzpěradla. Jelikož existuje přesné řešení této úlohy (odvození je možno nalézt v [3]), lze jej s výhodou užít.
V našem případě potřebujeme znát pouze vztah mezi sblížením konců vybočujícího prutu u (tj. vzdálenost o kterou se přiblíží konce prutu vlivem vybočení) a vzpěrnou silou N (působící ve směru spojnice konců prutu). Řešení odvozené v [3] ovšem takový vztah explicitně nenabízí a je potřeba tuto závislost řešit iterativně. Na počátku je volba pootočení konce vybočeného prutu 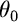, které figuruje v tomto řešení jako parametr, jenž měníme v průběhu iterace. Je-li zvoleno 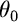, pak stačí vyřešit postupně následující dílčí výrazy (převzato z [3]):
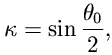 | (1) |
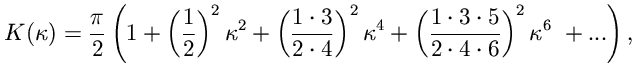 | (2) |
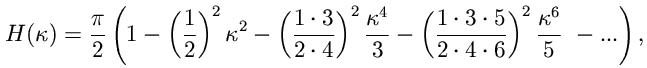 | (3) |
které užijeme pro stanovení hledaných veličin:
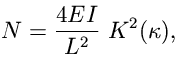 | (4) |
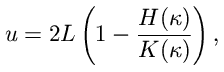 | (5) |
popřípadě i pro (zde nepotřebné) vzepětí prutu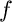 
(maximální příčné vybočení):
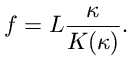 | (6) |
3 Pokritické tvary
Bylo zjištěno (například dle článků [1] a [2]), že štíhlé symetrické vzpěradlo může ztrácet stabilitu v zásadě dvojím způsobem. Bud' symetrickou napjatostí [1] nebo nesymetrickou napjatostí [2], viz obr. 2. Pro symetrickou napjatost jsou oba pruty ve shodném pokritickém stavu, kdežto při nesymetrické napjatosti je jeden prut v prekritickém stavu a druhý v pokritickém. Dalším možným rozlišením geometrie pokritických tvarů může být směr vybočení prutů, který se ovšem nijak neprojeví na napjatosti vzpěradla. Možné pokritické tvary jsou zobrazeny bez svých symetrických protějšků na obrázku 2.
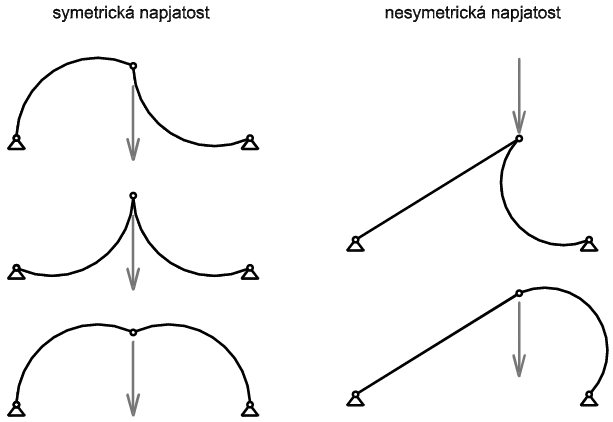
Figure 2: Pokritické tvary
4 Parametrická studie
Předcházející části tohoto článku shrnuly již publikované. Nyní přistupme ke studii vlivu změny výšky vzpěradla h na jeho pokritické působení. Na obrázku 3 je znázorněna reprezentační skupina vybraných vzpěradel (lišících se poměrem h/L, který charakterizuje dané vzpěradlo), jejichž řešení si zobrazíme.
Figure 3: Reprezentační skupina vzpěradel včetně charakteristického poměru h/L
Pro každé vzpěradlo z této reprezentační skupiny je vyřešena odděleně symetrická a nesymetrická napjatost (tj. zatěžovací síla F vs. svislý posun středního kloubu w) dle předpokladů definovaných výše s pomocí popsaného přesného řešení (4) a (5). Na obr. 4 je vidět graf pokritického působení vzpěradel při symetrické napjatosti (ve smyslu symetrie je zobrazena pouze levá část funkcí; transformováno do bezrozměrného tvaru).
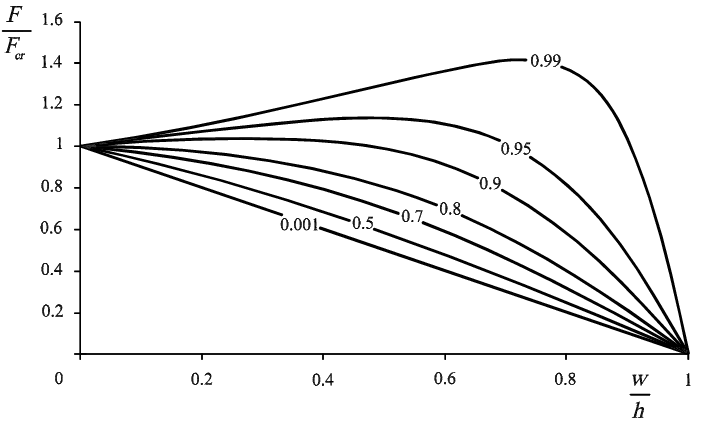
Figure 4: Funkce symetrické napjatosti
Z grafu na obrázku 4 je patrný vývoj napjatosti od nestabilního průběhu (klesající funkce) pro nízká vzpěradla, až po částečně stabilní průběh (nemonotónní funkce) vysokých vzpěradel. Lze říci, že stabilita symetrické napjatosti vzpěradla roste s jeho výškou (přesněji roste s růstem jeho poměru h/L). Za povšimnutí stojí rovněž degenerace napjatostní funkce do lineárního průběhu pro velmi nízká vzpěradla.
Pro nesymetrickou napjatost je situace poněkud složitější, viz graf na obrázku 5. Tento způsob ztráty stability se vyskytuje pouze pro vysoká vzpěradla (v grafu jsou vidět funkce pro vzpěradla s poměrem h/L 
0.7). Bylo vypočteno, že minimální výška vzpěradla h pro existenci nesymetrické napjatosti je přibližně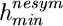 
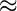0.5774 L.
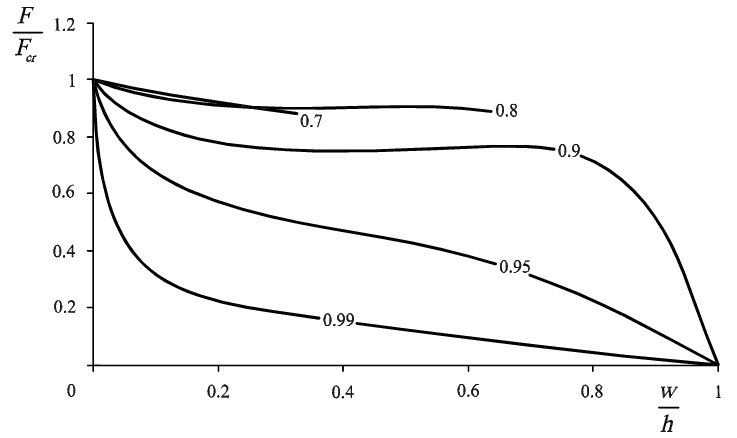
Figure 5: Funkce nesymetrické napjatosti
Z grafu na obr. 5 je také patrné, že pro určité hodnoty poměru h/L vyjadřujícího výšku vzpěradla existuje jistá kritická hodnota svislého posunu w, při které dojde k pádu nesymetrické napjatosti (řešení přestane náhle existovat). U reálného vzpěradla se to projeví přechodem na symetrickou napjatost.
4.1 Kritický posun
Označme kritický posun pro pád nesymetrické napjatosti wcr. V grafu na obr. 6 je zobrazen průběh funkce této kritické hodnoty wcr v závislosti na výšce vzpěradla h. Čárkovaná čára vymezuje horní limit wcr = h pro tento kritický posuv. Dosáhne-li wcr tohoto limitu, pak zřejmě nedochází k pádu nesymetrické napjatosti, protože poloha středního kloubu vzpěradla se při posunu w = h dostává mimo spojnici kloubových podpor. Tedy pro limitní výšku vzpěradla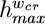 
pro existenci pádu nesymetrické napjatosti (shodnou zároveň s maximálním kritickým posunem wcr, max) z podmínky rovnosti délky L a vzdálenosti podpor platí:
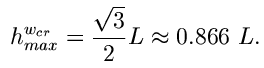 | (7) |
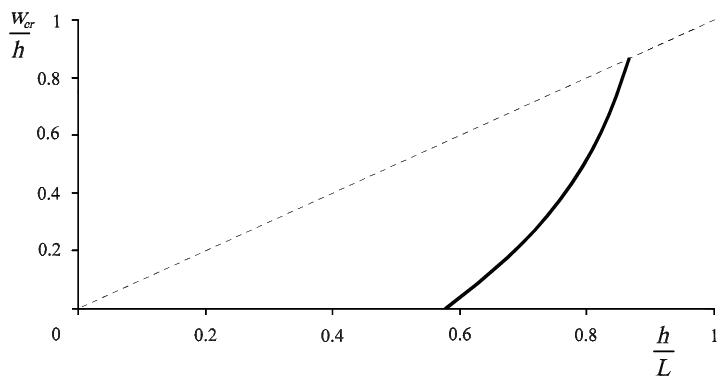
Figure 6: Průběh kritického posunu wcr pro pád nesymetrické napjatosti
5 Závěr
Vzpěradlo, jako příklad velmi jednoduché konstrukce, se ukazuje být komplikovanou úlohou v případě, že se jej rozhodneme řešit obecněji (s uvážením velkých deformací). V článku bylo ukázáno rozložení možných stavů při pokritickém působení s ohledem na proměnlivou výšku vzpěradla. Vzhledem k zjištěným skutečnostem je třeba říci, že bude dále vhodné prozkoumat energetickou bilanci nalezených řešení pro pochopení přechodů mezi symetrickou a nesymetrickou napjatostí vyšších vzpěradel.
Poděkování
Tento příspěvek byl vytvořen v rámci výzkumného záměru MSM 261100007 a s podporou grantu GA ČR 103/03/0233 a nadace Preciosa.
References
Frantík, P.: Jednostupňový model vzpěradla: Zpřesnění pokritického řešení, seminář Modelování v mechanice 2003, VŠB-TU Ostrava, leden 2003
Frantík, P.: Nesymetrické pokritické řešení vzpěradla, seminář Modelování v mechanice 2003, VŠB-TU Ostrava, leden 2003
Ržanicin, A., R.: Ustojčivost' ravnovesija uprugich sistem, Gosudarstvennoje izdatel'stvo techniko-teoretičeskoj literatury, Moskva 1955