Petr FRANTÍK, Institute of Structural Mechanics, Faculty of Civil Engineering, Brno University of Technology, Czech Republic
Jiří MACUR, Institute of Computer Aided Engineering and Computer Science, Faculty of Civil Engineering, Brno University of Technology, Czech Republic
The derivation of equations of motion of the special cantilever beam model is presented in the paper. The model is created for experimental research of dynamic behaviour of the harmonically loaded slender elastic beam. Very large displacements problems and stability problems (static and dynamic) were expected.
The model is special, because the special discretization method was used. If we consider very slender beam, then the bending oscillations play dominant role in the beam motion. It is possible to neglect the "normal" and the shear strain of the beam and use the "bending" strain only (there are quotes, because both effects are caused by normal strain). With this neglection, we can divide the beam into finite number of the physical absolutely rigid segments, which are connected by the hinges with the elastic (or arbitrary another) rotational springs, see fig. 1.
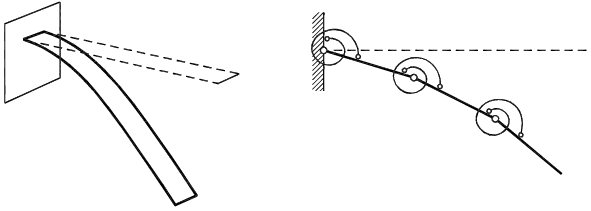
Fig. 1: Real structure and its special model
The neglection of the "normal" and the shear strain causes the increase of the calculations effectiveness and the expressive decrease of the calculations time cost. There is way to fast calculate wide problems with the static and dynamic stability of the beam with arbitrary load and the another nonlinear problems.
The derivation of the model equations of motion give the basic (it means without damping and without any external load) equation system (1):
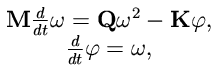| (1) |
where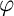 
is the vector of the segment rotations, 
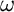is the vector of the segment angular velocities, M is the full symmetric matrix of the moments of inertia, Q is the similar full antimetric matrix and K is the three-diagonal bending stiffness matrix.
The equation system (1) of the model can be simple solved by explicite numerical methods (e.g. Euler method, Runge-Kutt method).
Acknowledgement: The research is provided under Czech research project CEZ: J 22/98: 261100009 and supported by grant No. 103/03/0233 from the Grant Agency of the Czech Republic.