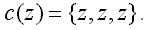
1. Úvod
Grafické zobrazování dat je důležitou součástí jakéhokoliv poznávacího procesu nad těmito daty. Je zřejmé a výzkumy potvrzené, že člověk je mnohem více citlivý na grafickou informaci, nežli na informaci v textové formě. V současnosti máme pro zobrazování dat běžně k dispozici barevné plošné zobrazovací prostředky a je otázkou času, kdy budeme mít možnost zobrazovat data přímo trojrozměrně.
Mějme libovolnou funkci f dvou proměnných x a y. Položme rovinu nezávislých proměnných do zobrazovací roviny. Úkolem je volba jednoznačné barevné škály, vyjadřující funkční hodnotu z = f (x,y) danou nezávislými proměnnými x, y ze zobrazovací roviny. Pro jednoduchost uvažujme, že obor hodnot funkce f je interval <0,1>.
2. RGB prostor barev
Uvažujme standardní Red-Green-Blue (červená-zelená-modrá) barevný model. Každá barva je v něm jednoznačně dána třemi hodnotami -- základními složkami -- červenou, zelenou a modrou. Tento model lze interpretovat jako omezený prostor se třemi rozměry, které odpovídají složkám barvy. Každý bod v tomto prostoru je potom unikátní barvou. Každá ze tří složek barvy nechť je reálné číslo z intervalu <0,1>. RGB prostor je potom krychle o jednotkové straně, viz obr. 1.
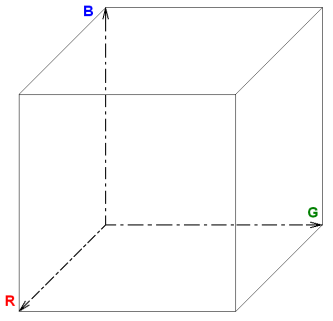
Obr. 1: krychle RGB prostoru
Pro tento barevný model platí, že hodnota složky barvy je úměrná jasu složky barvy, tj. barva {0,0,0} je černá a barva {1,1,1} je bílá. Pro lepší přiblížení k pochopení rozložení barev v tomto prostoru lze zobrazit např. barvy na podstavných plochách krychle. Toto zobrazení je vidět na obr. 2.
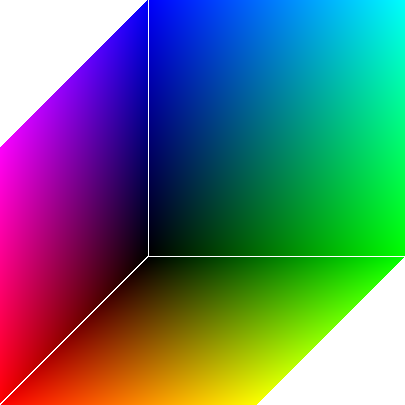
Obr. 2: Znázornění RGB prostoru (zobrazeny barvy na podstavných rovinách)
Z obrázku 2 je patrné, že s narůstající vzdáleností barvy od počátku (černé barvy) vzrůstá její jas. Tedy barvy se stejným objektivním jasem tvoří výsek kulové plochy se středem v počátku a nejjasnější barvou je barva bílá, ležící vzhledem k počátku na protilehlém vrcholu krychle. Monochromatická stupnice tvoří v této krychli uhlopříčku mezi černou {0,0,0} a bílou {1,1,1}. Z toho vyplývá, že pro monochromatickou stupnici jsou si hodnoty všech tří složek rovny (např. šedá barva může být dána bodem {0.5,0.5,0.5}).
RGB model se hodí pro zobrazovací proces, který barvy zobrazuje svícením (obrazovky, displeje). Pro tisk na papír se užívá inverzní model Cyan-Magenta-Yellow (azurová-fialová-žlutá), zkráceně CMY, jehož zobrazení je vidět na obrázku 3.

Obr. 3: Znázornění inverzního CMY prostoru (zobrazeny barvy na podstavných rovinách)
Zobrazené barevné modely na obr. 2 a obr. 3 se vzájemně doplňují. Z těchto dvou obrázků můžeme složit celý obal krychle obou prostorů.
3. Monochromatická stupnice
Nyní, když známe RGB prostor barev, můžeme hledanou barevnou stupnici chápat jako trajektorii v tomto prostoru. Například nejjednodušší již výše zmíněnou monochromatickou stupnici lze definovat jako úsečku mezi černou a bílou barvou, viz obr. 4.
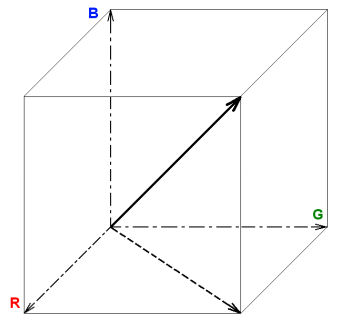
Obr. 4: Trajektorie monochromatické stupnice
Zapíšeme-li hledanou polohu bodu v RGB prostoru pomocí jednoho parametru z, který vyjadřuje stupnicí zobrazovanou funkční hodnotu, dostáváme barvu c (z):
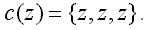 | (1) |
Tato stupnice je zobrazena na obr. 5.

Obr. 5: Monochromatická stupnice
Délka trajektorie této stupnice je přibližně 1.73. Závažnou nevýhodou této stupnice (kromě toho, že má krátkou trajektorii) je, že nemá konstantní jas. Oko je více citlivé na změnu barvy, než na změnu jasu. Proto jsou barevné stupnice s méně proměnným jasem výhodnější.
4. Bilineární stupnice
Jednoduchou barevnou stupnici s dlouhou trajektorií můžeme vytvořit tak, že povedeme úsečku z červeného vrcholu do zeleného vrcholu a dále ze zeleného vrcholu do modrého vrcholu, viz obr. 6. Délka trajektorie tak bude činit přibližně 2.83.
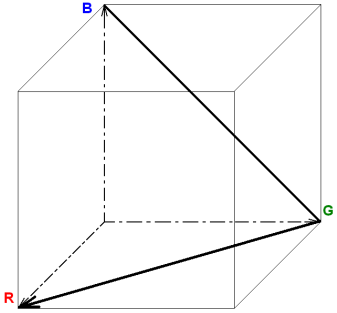
Obr. 6: Trajektorie bilineární stupnice
S pomocí jednoho parametru z, který vyjadřujícího zobrazovanou funkční hodnotu, dostáváme barvu c (z):
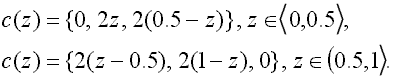 | (2) |
Tato stupnice je zobrazena na obr. 7.

Obr. 7: Bilineární stupnice
Nevýhodou této stupnice je, obdobně jako u předchozí, pokles jasu. Pro hodnoty z okolo 0.25 a 0.75 se jas barvy znatelně snižuje.
5. Bicirkulární stupnice
Předchozí bilineární stupnici můžeme snadno vylepšit nahrazením úseček kružnicovými oblouky, viz obr. 8. Dosáhneme tím konstantního objektivního jasu stupnice a navíc prodloužíme trajektorii na délku přibližně 3.14.
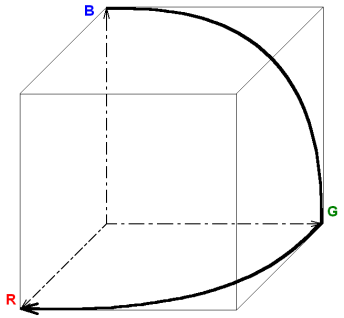
Obr. 8: Trajektorie bicirkulární stupnice
S pomocí jednoho parametru z, který vyjadřujícího zobrazovanou funkční hodnotu, dostáváme barvu c (z):
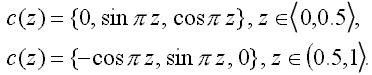 | (3) |
Tato stupnice je zobrazena na obr. 9.

Obr. 9: Bicirkulární stupnice
Nevýhodou této stupnice je, že obsahuje v popisu složitější funkce. Nevýhodná je rovněž vlastnost způsobená zalomením trajektorie: celá polovina trajektorie je v oblasti s převahou zelené složky (můžeme mluvit o jisté barevné nevyváženosti).
6. Eliptická stupnice
Tato stupnice je eliptickým obloukem v RGB prostoru, přičemž leží v rovině rovnoběžné s osou zelené složky, procházející červeným a modrým vrcholem (viz obr. 10). Částečně řeší problém nastíněný u předchozí stupnice. Má délku přibližně 2.70.
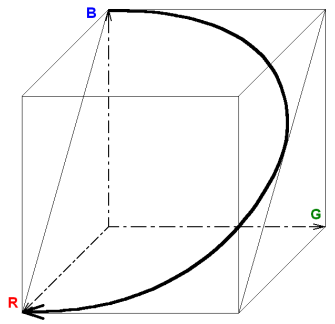
Obr. 10: Trajektorie eliptické stupnice
S pomocí jednoho parametru z, který vyjadřujícího zobrazovanou funkční hodnotu, dostáváme barvu c (z):
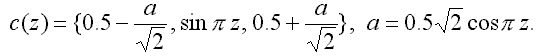 | (4) |
Tato stupnice je zobrazena na obr. 11.

Obr. 11: Eliptická stupnice
Nevýhodou této stupnice je, obdobně jako u předchozí, že obsahuje v popisu složitější funkce. Také je z obr. 11 patrné, že zelená barva je ve stupnici relativně slabě výrazná.
6. Závěr
Závěrem srovnejme popsané stupnice. Na obr. 12 jsou zobrazeny všechny čtyři stupnice dohromady. Z tohoto srovnání jsou patrné rozdíly mezi jednotlivými trajektoriemi.

Obr. 12: Srovnání stupnic
Poznamenejme, že délka trajektorie, jak je u každé stupnice uvedena, má souvislost s počtem barev, které v diskrétním zobrazení na počítači hrají roli rozlišení. Tj. máme-li zobrazovací rovinu o velikosti 500 krát 500 pixelů a zobrazíme-li funkci nad touto zobrazovací rovinou v monochromatické stupnici s 8-bitovou hloubkou, bude mít funkční hodnota rozlišení jen 256 vrstev. Užijeme-li barevné stupnice, dosáhneme rozlišení přes 500 vrstev díky delší trajektorii (např. bilineární stupnice má v 24-bitové hloubce (ekvivalent 8-bitové monochromatické) 511 vrstev). Tato výhoda, výhoda méně proměnlivého jasu a výraznější odlišení sousedních stupňů, je zřejmě rozhodující při volbě zobrazovacích stupnic.