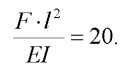
Abstract
Other stable bending shapes of cantilever beam loaded by force are described in this paper. Special dynamic nonlinear model is used. Energetic situation is investigated. First and second bending shapes are compared with experimental results.
Keywords
Cantilever beam, bending shapes, nonlinear solution, experimental results.
1. ÚVOD
Tento článek volně navazuje na příspěvek [1], který se věnoval přibližnému řešení průhybu štíhlého konzolového nosníku konstantního průřezu zatíženého silou v oblasti velkých deformací, ale malých přetvoření. Zde je tento řešený problém dále rozvinut. Některé důležité výsledky jsou ověřeny experimentem.
2. ÚLOHA
Mějme štíhlou prutovou konstrukci - konzolový nosník, zatížený na volném konci svislou, libovolně velkou silou, viz obr. 1. Předpokládejme, že prut je vždy dostatečně štíhlý, aby jeho materiál vykazoval lineárně pružné chování. Tento požadavek lze realizovat, nicméně vzniká experimentální problém s vlivem vlastní tíhy.
Předpokládejme dále, že vliv normálových a posouvajících sil na posunutí bodů prutu můžeme zanedbat. V takovém případě postačují k identifikaci prutu pouze dva parametry: délka prutu l a ohybová tuhost prutu EI. Dále zobrazené grafy řešení mají bezrozměrné osy a proto na hodnotách těchto parametrů nebude záležet. Vzhledem k tomu, že byl proveden náročný experiment, uveďme, že se jedná o prut ocelový, s délkou l=0.718 m a s ohybovou tuhostí EI=0.127 Pa.m4.
3. ŘEŠENÍ ÚLOHY
Úlohu řešme nahrazením prutu konečným počtem tuhých dílců spojených klouby s lineární rotační pružinou. Pro takto nahrazený prut jsou odvozeny pohybové rovnice - řešení je nalezeno dynamicky, hledáním ustáleného stavu dynamického systému. Protože jsou pohybové rovnice nelineární, využívá se k řešení numerická metoda - upravená Eulerova metoda.
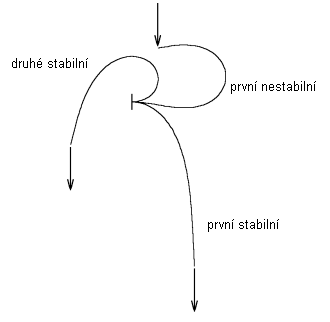
Nestabilní řešení úlohy (viz obr. 2) je nalezeno pomocí statické formulace naznačené náhrady, vyřešenou iterační Newtonovou metodou.
První stabilní řešení úlohy (viz obr. 2) bylo nalezeno tak, že se nezdeformovaný tlumený model konzoly zatížil silou F a nechal se dostatečně dlouhou dobu ustalovat. Ustálený stav lze vzít jako statické řešení úlohy.
Pro hledání dalších řešení byl zvolen speciální postup. Numerická metoda se destabilizovala velkým zvýšením síly F. Destabilizací metody se dosáhlo velkých rotací tuhých dílců a tím byl obdržen složitý "zamotaný" počáteční stav. Tlumení bylo zvýšeno a síla se snížila na požadovanou hodnotu. Po určité době se tak obnovila stabilita numerické metody a tlumení pak bylo sníženo.
4. DRUHÉ STABILNÍ ŘEŠENÍ
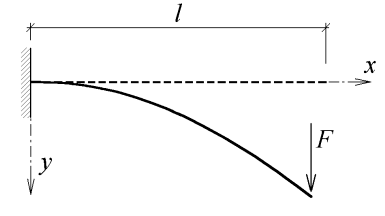
Ve zmíněném předcházejícím článku [1] bylo rozebráno nelineární řešení, které je prvním stabilním řešením této úlohy. Vedlejším produktem uvedeného odvození bylo také nalezení prvního nestabilního řešení, což před-znamenalo existenci druhého stabilního řešení. Na obr. 2 jsou naznačena tato tři řešení pro shodnou sílu danou vzorcem:
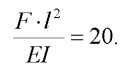| (1) |
První stabilní řešení úlohy existuje pro sílu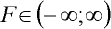 
, oproti tomu druhé stabilní řešení vyžaduje sílu F v absolutní hodnotě větší než jistá minimální hodnota, označme ji F2min, pro kterou přibližně platí:
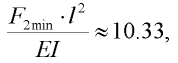 | (2) |
přičemž pro odpovídající svislé posunutí y2min koncového bodu konzoly vzhledem k vetknutí bude přibližně:
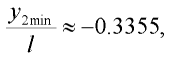 | (3) |
což znamená, že konec konzoly je nad bodem vetknutí.
Vztah mezi silou F a svislým posunutím koncového bodu y pro obě stabilní řešení je včetně experimentálních výsledků znázorněn na obr. 3.
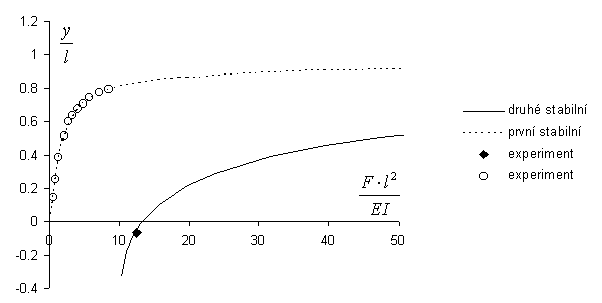
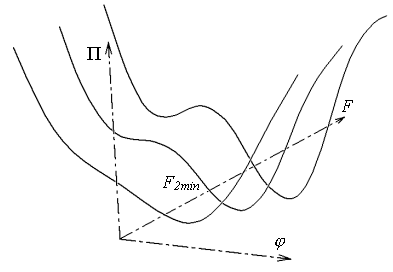
Je zajímavé, že druhé stabilní řešení dává při nízké velikosti síly F polohu koncového bodu konzoly nad bodem vetknutí. Z tohoto faktu vyplývá, že celková potenciální energie systému pro toto řešení je kladná, což je neobvyklé. Energetickou situaci kolem minimální síly druhého stabilního řešení F2min lze dobře znázornit funkcemi celkové potenciální energie 
jednostupňového modelu konzoly [2]. Jediným stupněm volnosti tohoto modelu je pootočení 
koncového bodu konzoly. Celková potenciální energie se pak mění pouze se změnou pootočení a se změnou velikosti síly F, viz obr. 4.
jednostupňového modelu [2] v závislosti na pootočení a na velikosti síly F
Na obr. 4 je vidět globální minimum prvního stabilního řešení. Je zde také patrný vývoj horního lokálního minima potenciální energie, které zaniká při snížení velikosti síly F pod hranici minimální hodnoty F2min. Toto minimum představuje druhé stabilní řešení. Současně vzniká také lokální maximum, které je nestabilním řešením úlohy a zaniká současně s druhým stabilním řešením (jsou spolu nedílně spjaty).
5. DALŠÍ ŘEŠENÍ
Popsaným postupem lze nalézt i další řešení této úlohy (výběr viz obr. 5). Řešení se smyčkami se jeví jako velmi málo stabilní. Je zajímavé, že smyčky jsou stabilnější, když systém kmitá, než když je v klidu.
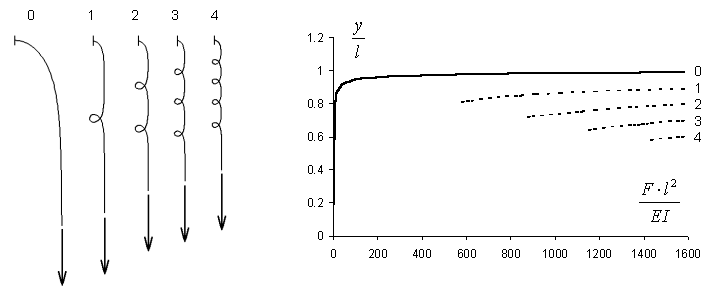
Na grafu na obr. 5 jsou spolu s průběhy znázorněny minimální dosažené hodnoty síly F pro jednotlivé počty smyček. Tyto minimální hodnoty je však potřeba vzít s rezervou, protože v jejich okolí je stabilita smyček nejistá.
6. Závěr
Bylo ukázáno, že ohyb konzolového nosníku má obecně více řešení. Výpočetně i experimentálně byla prokázána existence dvou stabilních řešení úlohy a naznačena další možná řešení, jejichž stabilitu bude vhodné výpočetně a experimentálně ověřit. S ohledem na vlastnosti studované úlohy (jednoduchý ohýbaný prut) lze očekávat podobné problémy i v případě složitějších prutových soustav.
Poděkování
Tento příspěvek je vytvořen v rámci výzkumného záměru CEZ: J22/98: 261100009.
Literatura
[1] Frantík P., Nelineární řešení průhybu konzoly, 4. odborný seminář doktorského studia, VUT FAST v Brně, Brno, únor 2002
[2] Frantík P., Sledování a simulace nelineární dynamické konstrukce, 3. odborný seminář doktorského studia, VUT FAST v Brně, Brno, únor 2001