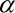sklon odlehčeného prutu, 
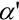sklon prutu po deformaci, N normálová síla v prutu.
1. Úvod
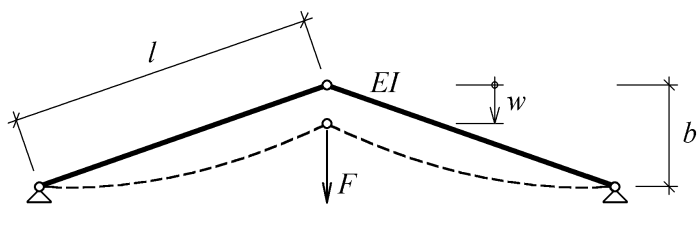
Vzpěradlo je jednoduchá symetrická staticky určitá konstrukce znázorněná na obr. 1. Je složena ze dvou přímých prutů spojených klouby a uložených kloubově neposuvně. Na této konstrukci lze dobře analyticky demonstrovat bohatou geometrickou nelinearitu úlohy, což v případě složitějších konstrukcí je zpravidla mnohem obtížnější. Tato konstrukce byla v minulosti řešena, přesto však zůstává předmětem zájmu jako příklad komplikované úlohy stavební mechaniky.
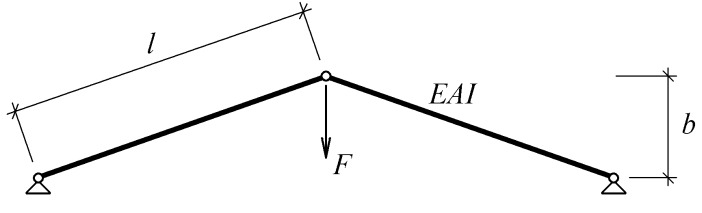
Obr. 1: Symerické vzpěradlo s vyznačenými parametry: l délka prutů, b výška středního kloubu vzpěradla, E modul pružnosti prutů, A plocha průřezu prutů a I moment setrvačnosti prutů.
2. Řešení
Vzpěradlo na obr. 1 je zatíženo svislou silou v prostředním kloubu. Nás bude zajímat vztah mezi velikostí této síly F a svislou deformací (posunutím) prostředního kloubu, označíme ji w. Řešení si přípustně zjednodušíme tím, že budeme odděleně uvažovat různé způsoby přetvoření prutů. Toto zjednodušení nám totiž značně pomůže v nalezení hledaného vztahu.
3. Normálové stlačení/protažení prutů
Uvažujme, že se pruty po zatížení pouze zkrátí či prodlouží (zůstávají po deformaci přímé). Situaci lze znázornit obr. 2:
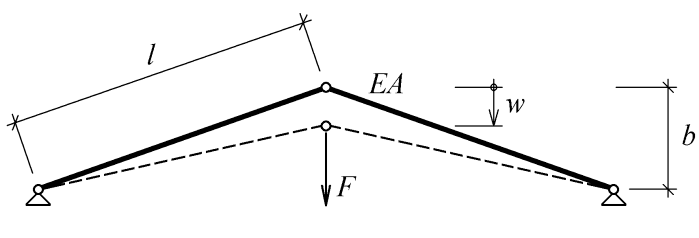
Obr. 2: Vzpěradlo po normálovém stlačení prutů (tučně odtížený stav, čárkovaně stav po deformaci)
Pro nalezení řešení takto formulované úlohy můžeme konstrukci řešit nejlépe v deformovaném stavu. Situace statických a geometrických podmínek je naznačena s využitím symetrie na levé polovině vzpěradla, viz obr. 3:
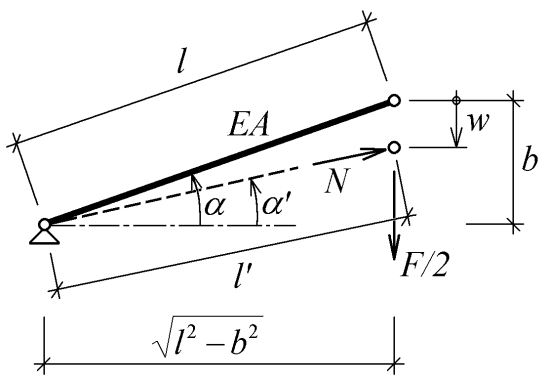
Obr. 3: Detail levé poloviny vzpěradla (s využitím symetrie) s označením: EA normálová tuhost prutu, l' délka prutu po deformaci (po zatížení), 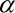sklon odlehčeného prutu, 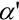sklon prutu po deformaci, N normálová síla v prutu.
Pro vnitřní normálovou sílu N v prutu musí platit podmínka rovnováhy ve středním kloubu:
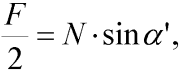 | (1) |
přičemž platí:
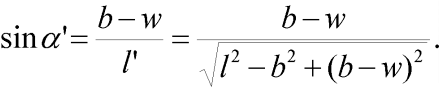 | (2) |
Pro sílu N také za předpokladu lineárně pružného materiálu můžeme psát:
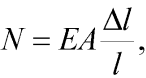 | (3) |
přičemž platí:
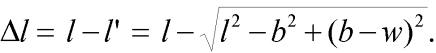 | (4) |
Vztah (3) použijeme k dosazení za vnitřní sílu N do vztahu (1) a po vyjádření velikosti zatěžující síly F s využitím vztahů (2) a (4) můžeme obdržet:
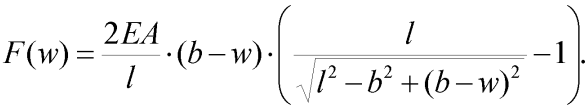 | (5) |
což je hledaná závislost pro zvolený způsob deformace. Graf této závislosti je na obr. 4:
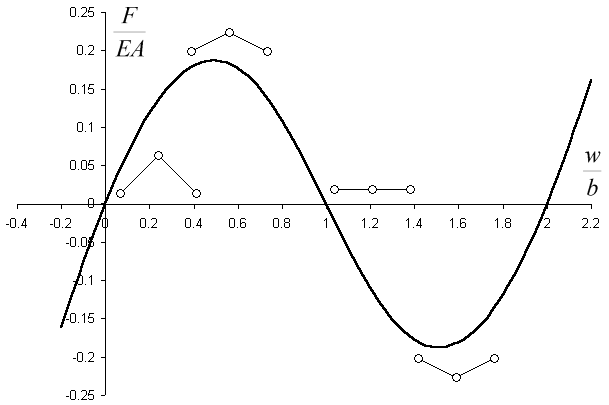
Obr. 4: Graf závislosti síly F na průhybu w s bezrozměrnými osami pro l=b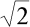
(prut vzpěradla tvoří v odlehčeném stavu úhlopříčku čtverce).
Z grafu na obr. 4 je patrné, že pro tento druh přetvoření prutů probíhá zatěžování postupně vzrůstající silou poklidně až do lokálního maxima (průhyb w přibližně 0.5b). Po dosažení tohoto bodu se úloha destabilizuje a dochází k přeskoku vzpěradla na protilehlou (spodní) stranu. Po přeskoku probíhá zatěžování opět poklidně.
V případě, že zatěžujeme vzpěradlo deformací středního kloubu, je úloha stále stabilní.
4. Vybočení prutů
Uvažujme, že pruty po zatížení vybočí. Situaci lze znázornit obr. 5:
Obr. 5: Vzpěradlo po symetrickém vybočení prutů (tučně odtížený stav, čárkovaně stav po deformaci)
Tento druhý způsob deformace vzpěradla je poněkud složitější (k pochopení souvislostí je třeba znát problematiku vzpěru prutu, viz [1],[2]). Analyticky jej zde vyřešíme pouze přibližně s užitím klasického řešení vzpěru prutu. Z Eulerova klasického řešení vyplývá, že k vybočení prutu je zapotřebí, aby síla, zatěžující prut ve směru spojnice jeho konců, dosáhla kritické síly Ncr, pro kterou platí:
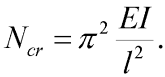 | (6) |
Situace v okamžiku dosažení kritické síly je naznačena na obr. 6 (je třeba poznamenat, že zobrazené schema je pouze přibližné - odpovídá klasickému řešení vzpěru prutu):
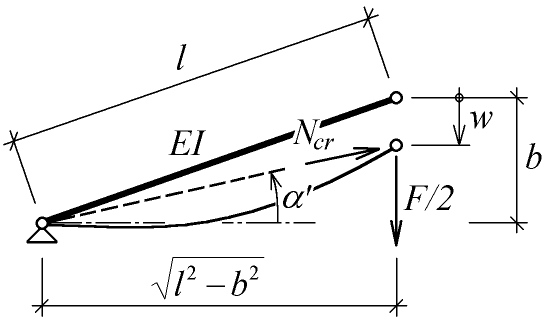
Obr. 6: Detail levé poloviny vzpěradla (opět s využitím symetrie) s označením: EI ohybová tuhost prutu.
Užité klasické řešení ale nedává žádnou informaci o hodnotě vybočení prutu (přesněji řečeno je tato hodnota neurčitá) a hodnotě sblížení konců prutu, což ovšem není na závadu (k získání těchto hodnot (alespoň jejich aproximací) je zapotřebí přesnějšího řešení, viz [3],[2]). Postačuje nám přibližná informace, že při libovolném vybočení prutu (sblížení konců prutu) je zatěžující síla rovna síle kritické Ncr. Z uvedeného vyplývá, že přibližně (ve smyslu klasického řešení) pro hodnotu průhybu w z intervalu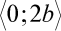 
platí:
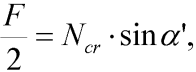 | (7) |
což lze s využitím vztahů (2) a (6) přepsat na:
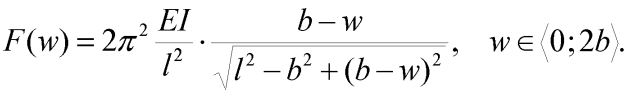 | (8) |
Tento odvozený vztah je hledanou závislostí pro ohybový způsob deformace vzpěradla. Lze jej nazývat pokritickým vztahem, protože platí jen za předpokladu dosažení (přesněji překročení) kritické síly v prutech vzpěradla. Neuvedenou podmínkou pro platnost tohoto vztahu je symetrie úlohy. Odvození předpokládá nezměněnou horizontální polohu středního kloubu, což není samozřejmé. Nicméně by se mělo podrobnějšímy výpočty prokázat, že tato symetrie (i pro antimetrické tvary vybočení prutů - např. levý prut vybočí dolů a pravý vybočí nahoru) zůstává zachována. Graf závislosti nalezené (8) je na obr. 7:
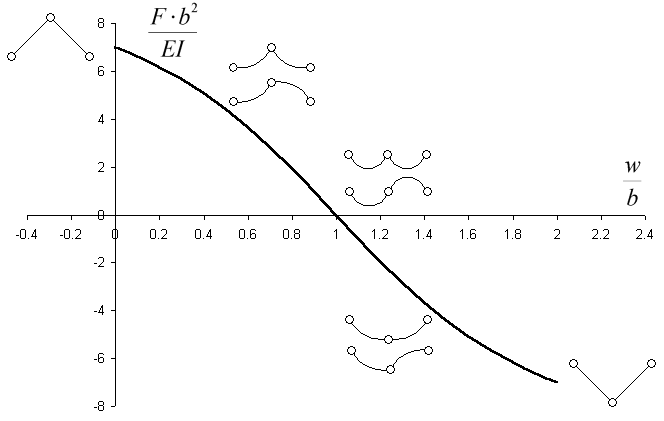
Obr. 7: Graf závislosti síly F na průhybu w s bezrozměrnými osami pro l=b (prut vzpěradla tvoří v odlehčeném stavu úhlopříčku čtverce).
5. Kombinace přetvoření
Uvažujeme-li o případu vzpěradla, u kterého proběhnou oba způsoby deformace (přetvoření) prutů, lze obě řešení vzájemně zkombinovat. Obdržíme tak závislost zobrazenou na grafu na obr. 8:
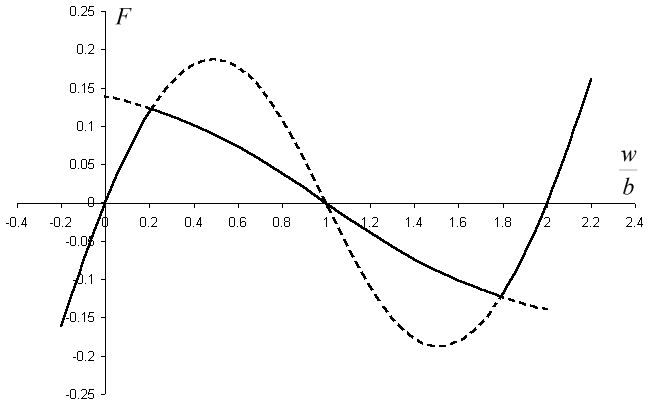
Obr. 8: Graf závislosti síly F na průhybu w pro fiktivní vzpěradlo s rozměry: výška b=1 m, délka prutů l= m (prut vzpěradla tvoří v odlehčeném stavu úhlopříčku čtverce), normálová tuhost EA=1 Pa.m2, ohybová tuhost EI=0.02 Pa.m4.
Zobrazenou závislost lze popsat: Pruty vzpěradla se při zvyšování zatěžující síly F pouze stlačují do okamžiku, kdy jejich normálová síla N dosáhne kritické síly Ncr (definované vztahem (6)). Při dosažení kritické síly dochází k vybočení prutů a vzpěradlo se destabilizuje. Po proběhnutí přechodového jevu, kdy vzpěradlo přeskočí na opačnou stranu dochází pouze k prodlužování prutů. Je zřejmé, že úloha v souladu s intuicí obsahuje symetrii: nezáleží na tom, zdali je vzpěradlo v dolní či horní poloze, čemuž odpovídá působení zatěžující síly zdola resp. zhora.
S pomocí vztahů (5) a (8) lze odvodit polohu kritického bodu, jako průsečík těchto funkcí. Pro polohu průsečíku lze takto odvodit:
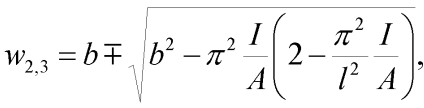 | (9) |
přičemž hodnota lokálně maximální síly (kritické síly vzpěradla) se stanoví dosazením do vztahu (5) nebo (8).
6. Závěr
Vzpěradlo je napohled jednoduchá konstrukce. Přesto kombinace vzpěru prutů a geometrie jejich vázaného pohybu dává chování, které ukazuje úskalí některých stavebně-mechanických systémů podrobených většímu zatížení, popřípadě větším deformacím.
Z naznačené přibližnosti odvození pokritického působení prutů vzpěradla lze vidět možnost hledání přesnějšího vztahu s využitím lepších aproximací řešení úlohy vzpěru prutu.
Řešeno bylo vzpěradlo dokonalé, tj. přímé pruty stejné délky a stejných fyzikálně-mechanických vlastností. Z úlohy vzpěru prutu je však patrné, že nedokonalosti (imperfekce) vzpěradla řešený problém změní a ještě více zkomplikují.
Literatura