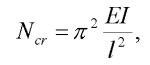
Abstract
Two unsymmetrical analytic solutions of strut truss (von Misess truss) are described in this paper.
1. Úvod
V článcích [1] a [2] je odvozeno symetrické pokritické řešení vzpěradla (tuto konstrukci lze nalézt popsanou také v [3] jako von Misesův nosník). Oprávněnost předpokladu symetrie je doložena numerickým výpočtem, přičemž byla ověřena i stabilita symetrického tvaru vůči ztrátě symetrie. Při hledání analytického důkazu nutnosti symetrie však bylo zjištěno, že statické podmínky nebrání současné existenci nesymetrického řešení. Tento příspěvek je věnován hledání tohoto řešení.
2. Úloha
Mějme jednoduchou rovinnou prutovou konstrukci znázorněnou na obr. 1. Je složena ze dvou šikmých prutů stejné délky a fyzikálně-mechanických vlastností. Tyto pruty jsou spojeny kloubem a uloženy kloubově neposuvně (viz obr. 1). Konstrukce je zatížena svislou silou působící v prostředním kloubu (převzato z článku [1]).
Zanedbejme práci posouvajících a normálových sil a uvažujme, že k deformaci vzpěradla dojde tehdy, když jeden prut vybočí (normálová síla v tomto prutu překročí hodnotu kritické síly) a druhý zůstane přímý (normálová síla v tomto prutu bude nižší než kritická síla). Z tohoto předpokladu vyplývá, že musí dojít k horizontálnímu posunu středního kloubu vzpěradla, a tedy bude porušena horizontální symetrie úlohy (viz obr. 2).
3. Klasické řešení
Eulerovo klasické řešení vzpěru prutu nám říká, že dosáhne-li hodnota normálové síly v prutu hodnoty kritické síly Ncr, pak dojde k vybočení prutu. Hodnoty vlastností vybočení jsou však neurčité. Lze říci, že při libovolném sblížení konců prutu bude prut působit silou N, ve směru spojnice jeho konců, rovnou kritické síle Ncr, pro kterou platí:
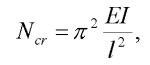| (1) |
kde l je délka prutu a EI je ohybová tuhost prutu.
V předchozí kapitole popsaný předpoklad o nesymetrii úlohy dává situaci, která je znázorněna na obr. 2. Vzhledem ke klasickému řešení můžeme o této situaci říci, že v levém prutu musí být síla N1 nižší než kritická síla Ncr a v pravém prutu síla N2 právě rovna síle kritické Ncr.
sklon levého prutu, 
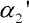sklon spojnice konců pravého prutu po vybočení prutu, x1, resp. x2, horizontální vzdálenost levého resp. pravého kloubu od středního kloubu po deformaci, 2a vzdálenost podpor vzpěradla, ľ2 vzdálenost konců pravého prutu po deformaci
Z horizontální silové podmínky rovnováhy na středním kloubu obdržíme vztah:
 | (2) |
přičemž pro hodnoty x1,, x2,, ľ2 dle obr. 2 platí:
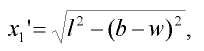 | (3) |
 | (4) |
 | (5) |
Z vertikální silové podmínky rovnováhy na středním kloubu pak obdržíme hledaný vztah:
 | (6) |
což lze za využití vztahu (2) a se známou rovností N2,klas=Ncr upravit na:
 | (7) |
4. Zpřesněné řešení
Výše užité klasické řešení je nejjednodušší možnou aproximací vybočeného prutu. Jak bylo řečeno, dává nám pouze malou informaci o vybočení prutu. Pro získání lepší aproximace působení vybočeného prutu lze užít speciální jednostupňový model popsaný v [4], [1]. Nahrazení pravého prutu jednostupňovým modelem je znázorněno na obr. 3.
je pootočení tuhého dílce vzhledem ke spojnici konců prutu, y2, je velikost vybočení prutu
Aplikací tohoto modelu (viz [4], [1]) na vybočený prut obdržíme zpřesněný vztah pro sílu N2, kterou vybočený prut působí na střední kloub (viz obr. 3):
 | (8) |
přičemž pro hodnotu vybočení prutu y2, platí vztah:
 | (9) |
Vztah (7) lze potom dosazením do (2) a (6) s využitím vztahů (8) a (9) upřesnit:
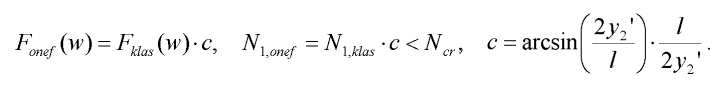 | (10) |
5. Srovnání
Nalezená nesymetrická řešení (7) a (10) si srovnáme mezi sebou a také se svými symetrickými protějšky odvozenými v [1] a [2]. Srovnání provedeme pro vysoké vzpěradlo, pro které platí l=1.2b v grafu s bezrozměrnými osami, viz obr. 4.
6. Závěr
Odvozená řešení naznačují zajímavé chování vzpěradla a zasluhovala by větší pozornost, která je ovšem nad rámec tohoto příspěvku. Navíc existence odvozených řešení souvisí s výškou vzpěradla. Platí, že čím nižší vzpěradlo, tím menší možnost existence nesymetrického řešení.
Řešeno bylo dokonalé vzpěradlo bez vlivu práce normálových a posouvajících sil. Zejména imperfekce, zlepšující popis skutečných konstrukcí, úlohu zkomplikují a ještě více obohatí.
Poděkování
Tento příspěvek je vytvořen v rámci výzkumného záměru CEZ: J22/98: 261100009 a s podporou grantu GA ČR 103/02/1030.
Reference
[1] Frantík P., Jednostupňový model vzpěradla: zpřesnění pokritického řešení, seminář Modelování v mechanice 2003, VŠB-TU Ostrava, leden 2003
[2] Frantík P., Řešení vzpěradla, uveřejněno na internetu na adrese: http://kitnarfovo.misto.cz/pub/2003.01.vzperadlo/vzperadlo.htm, leden 2003
[3] Bažant Z. P., Cedolin L., Stability of Structures, Oxford University Press, Oxford, 1991
[4] Frantík P., Jednostupňový model vzpěru prutu, uveřejněno na internetu na adrese: http://kitnarfovo.misto.cz/pub/2002.02.onefreed/onefreed.htm, únor 2002