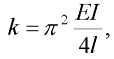
Jednostupňový model vzpěradla: Zpřesnění pokritického řešení

Petr Frantík

 

Abstract

Analytic solution of special one-degree-of-freedom model of strut-frame (von Misses truss) is described in this paper. The solution is also compared with numerical results.

 

1. Úvod

Vzpěradlo je známé již dlouho a je dobrým příkladem jednoduché konstrukce, která má komplikované řešení. Jeho geometrie umožňuje výrazné nelineární jevy i při malém zatížení. Důležitá výhoda vzpěradla je ve snadnosti nalezení přibližných analytických řešení. Zde je ukázáno odvození právě takového řešení v pokritické oblasti působení vzpěradla, které upřesňuje řešení vycházející z klasického řešení vzpěru prutu, odvozeného např. v [1].

 

2. Úloha

Mějme jednoduchou rovinnou prutovou konstrukci znázorněnou na obr. 1. Je složena ze dvou šikmých prutů stejné délky a fyzikálně-mechanických vlastností. Tyto pruty jsou spojeny kloubem a uloženy kloubově neposuvně (viz obr. 1). Konstrukce je zatížena svislou silou působící v prostředním kloubu.


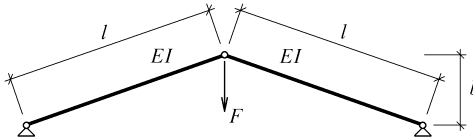
Obr. 1: Schéma vzpěradla s označením: l je délka prutů, EI je ohybová tuhost prutů, b je výška středního kloubu vzpěradla a F je velikost zatěžující síly

Zanedbejme práci posouvajících a normálových sil a uvažujme, že k deformaci vzpěradla dojde tehdy, když pruty vzpěradla vybočí.

 

3. Jednostupňový model

Předpokládejme, že při vybočení prutů vzpěradla se bude střední kloub pohybovat pouze po svislé přímce. Tento předpoklad není samozřejmý, ale dále uvedeným diskrétním numerickým řešením bylo prokázáno, že platí. Za této podmínky můžeme uvažovat pouze symetrickou polovinu vzpěradla - např. levý prut. Tento levý prut pak nahradíme jednostupňovým modelem, který je aplikací jednostupňového modelu vzpěru prutu [2], viz obr. 2.


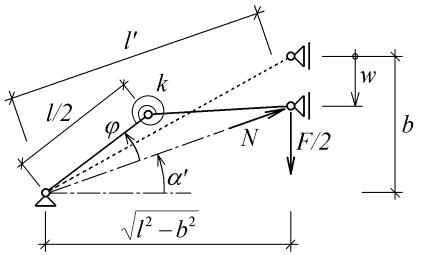
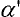Obr. 2: Detail nahrazení prutu jednostupňovým modelem s označením: l, vzdálenost konců prutu po vybočení, w posun středního kloubu vzpěradla, N síla kterou působí prut na střední kloub, sklon spojnice konců prutu po vybočení prutu, 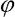pootočení dílce modelu vzhledem ke spojnici konců prutu, k tuhost náhradní lineární rotační pružiny

Jednostupňový model [2], kterým byl prut nahrazen, je složen ze dvou tuhých dílců spojených lineární rotační pružinou s tuhostí k danou vzorcem:

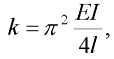(1)

která je stanovena tak, aby kritická síla jednostupňového modelu odpovídala kritické síle skutečného prutu, viz [2].

Sestavíme-li podmínku rovnováhy ve středním kloubu, dostáváme vztah pro sílu N, kterou působí vybočený prut na střední kloub:

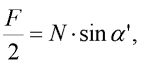(2)

přičemž pro úhel 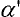platí:

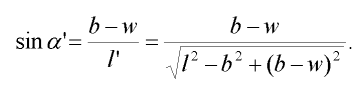(3)

Síla N je z odvození jednostupňového modelu vzpěru prutu [2] dána vztahem:

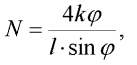(4)

přičemž pro úhel 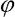platí dle obr. 2:

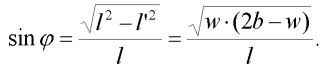(5)

Složením předcházejících vztahů obdržíme hledanou závislost:

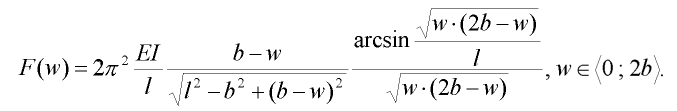(6)

 

4. Srovnání

Pro ověření a význam nalezeného řešení si provedeme jeho srovnání s řešením vycházejícím z Eulerova klasického řešení vzpěru prutu [1] a také s numerickým řešením metodou tuhých fyzických konečných prvků (zkratkou MTFKP, viz [3] a [4]), kterou bylo pro kontrolu řešeno celé vzpěradlo pro ověření symetrie úlohy. Metoda MTFKP nahrazuje prut konečným počtem tuhých dílců spojených klouby s lineárními rotačními pružinami. Na obr. 3 lze vidět touto metodou vypočtený pokritický tvar vzpěradla.


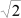Obr. 3: Pokritický tvar vzpěradla vypočtený metodou MTFKP prokazující předpoklad o zachování symetrie úlohy vzhledem k horizontální poloze středního kloubu; fiktivní vzpěradlo l=1 m, b= 1/m, EI=1 Pa.m4, F=4.55 N

Aplikací Eulerova klasického řešení vzpěru prutu obdržíme rovnici (odvozenou v [1]):

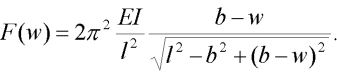(7)

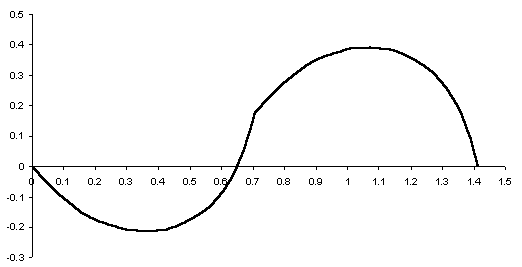
Srovnání funkcí (6), (7) a výsledků metody MTFKP je provedeno na obr. 4. Je potřeba uvést, že slabou implementací metody MTFKP se nepodařilo vypočtení celé závislosti vinou nestability úlohy. Proto je na obr. 4 nedostatečný počet vynesených bodů. Z obr. 4 lze také rozpoznat lepší výstižnost nově odvozeného řešení, ačkoliv při zvyšující se síle dochází k odklonu od trendu bodů vypočtených metodu MTFKP.


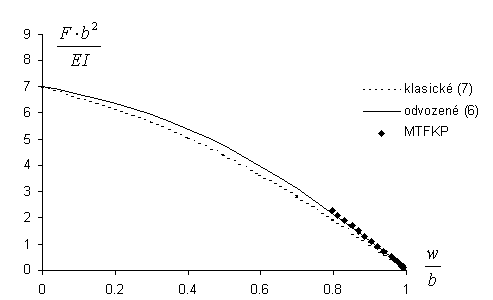
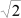Obr. 4: Graf srovnání analytických řešení a numerických výsledků výpočtu vzpěradla, které má délku prutů l=b (prut tvoří v odlehčeném stavu úhlopříčku čtverce); vyneseno v bezrozměrných osách

 

5. Závěr

Nalezené řešení pokritického působení vzpěradla je ve shodě s výsledky vypočtenými numerickou metodou MTFKP. Toto zlepšení bylo v souladu s dobrou výstižností jednostupňového modelu vzpěru prutu, popsaného v [2].

Zajímavým zjištěním je zachování symetrie úlohy. Tento fakt značně přispěl ke snadnosti analytického řešení úlohy. Z tohoto příkladu je vidět dobrá souhra užití analytického a numerického přístupu k řešení stavebně-mechanických úloh.

 

Poděkování

Tento příspěvek je vytvořen v rámci výzkumného záměru CEZ: J22/98: 261100009 a s podporou grantu GA ČR 103/02/1030.

 

Reference

[1] Frantík P., Řešení vzpěradla, uveřejněno na internetu na adrese: http://kitnarfovo.misto.cz/pub/2003.01.vzperadlo/vzperadlo.htm, leden 2003

[2] Frantík P., Jednostupňový model vzpěru prutu, uveřejněno na internetu na adrese: http://kitnarfovo.misto.cz/pub/2002.02.onefreed/onefreed.htm, únor 2002

[3] Henrych J., Úplná soustava finitních metod mechaniky a možnosti dalšího rozvoje, studie 6.85 ČSAV, Akademia 1985, Praha

[4] Frantík P., Diskrétní řešení vzpěru prutu, seminář Problémy modelování, VŠB-TU Ostrava, leden 2002

Ing. Petr Frantík, Ústav stavební mechaniky FAST VUT v Brně, Veveří 95, e-mail: kitnarf at centrum dot cz