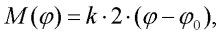
Abstract
Numerical simulation of simple model of the imperfect beam buckling is described in this paper. The beam is loaded by gravity and harmonic load. Phase portraits, limit cycles, strange attractor and its Poincare map are showed.
1. Úvod
Řešení nelineárních dynamických úloh vyžaduje ve složitějších případech, kdy je nelinearita úlohy významná, simulační přístup. Jinak řečeno, abychom poznali chování řešeného systému, musíme jeho vývoj v čase sledovat, tj. provádět jeho simulaci. Takto ovšem vznikají značné požadavky na výpočetní čas. Při rozsáhlejších studiích chování systému, kdy je zapotřebí mnoha jednotlivých simulací, nalézá uplatnění i velmi jednoduchý model.
2. Úloha
Mějme svisle orientovaný reálný štíhlý prut konstantního průřezu oboustranně kloubově uložený a zatížený na posuvném konci v čase harmonicky proměnlivou silou působící svisle na konci prutu (viz obr. 1). Uvažujme, že materiál prutu působí jako fyzikálně lineární (díky štíhlosti prutu nedosahujeme velkých přetvoření) a zanedbejme práci posouvajících a normálových sil na přetvoření prutu. Za těchto předpokladů lze vytvořit jednoduchý jednostupňový model, zobrazený spolu se svou předlohou na obr. 1.
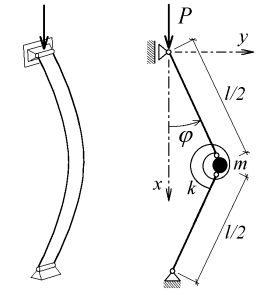
Prut je nahrazen soustředěnou hmotou o hmotnosti m a dvojicí tuhých dílců spojených kloubem s lineární rotační pružinou. Pružina působí na tuhé dílce momentem o velikosti:
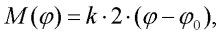 | (1) |
kde 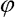 je pootočení dílce vzhledem ke svislé ose,
je pootočení dílce vzhledem ke svislé ose, 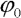 je imperfekce prutu uvažovaná jako počáteční pootočení (prut není dokonale přímý) a k je tuhost pružiny, pro kterou platí vzhledem ke kritické síle reálného prutu vztah [1]:
je imperfekce prutu uvažovaná jako počáteční pootočení (prut není dokonale přímý) a k je tuhost pružiny, pro kterou platí vzhledem ke kritické síle reálného prutu vztah [1]:
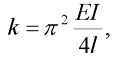 | (2) |
kde EI je ohybová tuhost prutu a l je délka prutu.
Prut je umístěn ve svisle působícím gravitačním poli s intenzitou g a na konec prutu působí proměnlivá síla, jejíž rovnice je dána předpisem:
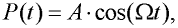 | (3) |
kde A je amplituda síly,  je kruhová frekvence a t je čas. Definujme navíc fiktivní celkovou sílu F jako součet amplitudy A síly P a tíhy m . g soustředěné hmoty m.
je kruhová frekvence a t je čas. Definujme navíc fiktivní celkovou sílu F jako součet amplitudy A síly P a tíhy m . g soustředěné hmoty m.
Pohybovou rovnici modelu můžeme za předpokladu útlumu lineárně závislého na rychlosti soustředěné hmoty psát ve tvaru:
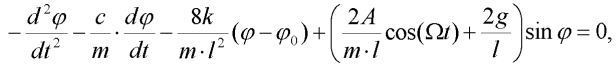 | (4) |
kde c je koeficient útlumu.
3. Simulace
Rovnice (4) je nelineární diferenciální rovnice druhého řádu. K jejímu řešení použijeme numerických metod pro řešení počátečního problému obyčejné diferenciální rovnice prvního řádu. Rovnici (4) proto upravíme do tvaru obvyklého pro řešení dynamických systémů:
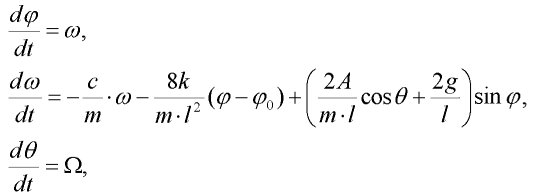 | (5) |
kde 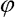 ,
, 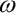 ,
, 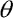 jsou stavové proměnné:
jsou stavové proměnné: 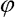 je úhlová výchylka,
je úhlová výchylka, 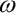 je úhlová rychlost a
je úhlová rychlost a 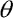 je fáze budící síly. Soustava (5) je soustavou tří diferenciálních rovnic prvního řádu, kterou budeme řešit Klasickou Runge-Kuttovou metodou. Tato metoda patří k základním metodám vhodným pro simulaci tlumených (disipativních) dynamických systémů a je postačující pro řešení vybraného systému (5).
je fáze budící síly. Soustava (5) je soustavou tří diferenciálních rovnic prvního řádu, kterou budeme řešit Klasickou Runge-Kuttovou metodou. Tato metoda patří k základním metodám vhodným pro simulaci tlumených (disipativních) dynamických systémů a je postačující pro řešení vybraného systému (5).
4. Parametry
Simulovat budeme úlohu s parametry: gravitační zrychlení g=9.81 m.s-2, koeficient útlumu c=0.1 N.s.m-1, hmotnost soustředěné hmoty m=0.21 kg, délka prutu l=0.723 m, tuhost pružiny k=0.3921 N.m.rad-1 a imperfekce 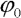 =0.005 rad (vlastní frekvence asi 0.2 Hz). Tyto parametry odpovídají zhruba štíhlému ocelovému prutu, který byl experimentálně staticky měřen ve vzpěru (viz článek [2]) a má kritickou sílu Fcr=2.17 N. S uvážením příspěvku soustředěné hmoty m je kritická hodnota amplitudy síly Acr=0.1099 N. Pro druhé stabilní řešení je minimální hodnota celkové síly přibližně Fmin=2.236 N, tedy amplituda Amin=0.176 N.
=0.005 rad (vlastní frekvence asi 0.2 Hz). Tyto parametry odpovídají zhruba štíhlému ocelovému prutu, který byl experimentálně staticky měřen ve vzpěru (viz článek [2]) a má kritickou sílu Fcr=2.17 N. S uvážením příspěvku soustředěné hmoty m je kritická hodnota amplitudy síly Acr=0.1099 N. Pro druhé stabilní řešení je minimální hodnota celkové síly přibližně Fmin=2.236 N, tedy amplituda Amin=0.176 N.
5. Fázové portréty
Pro ilustraci dynamiky chování systému v okolí kritické síly si zobrazíme fázové portréty systému v rovině 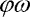 , přičemž bude pro frekvenci síly P platit
, přičemž bude pro frekvenci síly P platit  =0 (síla bude v čase neproměnná, fáze budící síly
=0 (síla bude v čase neproměnná, fáze budící síly 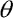 bude konstantní). Fázové portréty zobrazíme vždy ve dvojicích. Každá dvojice má shodnou velikost síly, ale jeden portrét ze dvojice bude pro systém netlumený a druhý pro systém s útlumem. Pozice portrétů vzhledem ke statickému řešení úlohy je naznačena v bifurkačním diagramu na obr. 2.
bude konstantní). Fázové portréty zobrazíme vždy ve dvojicích. Každá dvojice má shodnou velikost síly, ale jeden portrét ze dvojice bude pro systém netlumený a druhý pro systém s útlumem. Pozice portrétů vzhledem ke statickému řešení úlohy je naznačena v bifurkačním diagramu na obr. 2.
 v závislosti na celkové vzpěrné síle F s vyznačením pozice fázových portrétů
v závislosti na celkové vzpěrné síle F s vyznačením pozice fázových portrétů
Fázový portrét A=0.09 N (F=2.15 N): prekritický stav
Před dosažením kritické síly má vzpěr reálného prutu jediné řešení, jehož poloha (vyjádřená hodnotou celkové úhlové výchylky 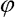 ) se s blížící kritickou silou stále rychleji vzdaluje od počáteční hodnoty. Na obr. 3 je vidět dvojice portrétů, netlumený a tlumený, na nichž je dobře patrná existence jediného řešení.
) se s blížící kritickou silou stále rychleji vzdaluje od počáteční hodnoty. Na obr. 3 je vidět dvojice portrétů, netlumený a tlumený, na nichž je dobře patrná existence jediného řešení.
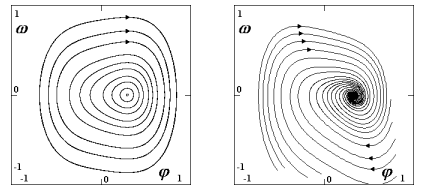
Fázový portrét A=0.15 N (F=2.21 N): postkritický stav (existuje jediné řešení)
Fázové portréty na obr. 4 jsou z oblasti po dosažení kritické síly, těsně před vznikem druhého stabilního řešení. Na portrétech je rozpoznatelný zárodek druhého stabilního řešení: V levé části portrétů se zakřivují trajektorie.
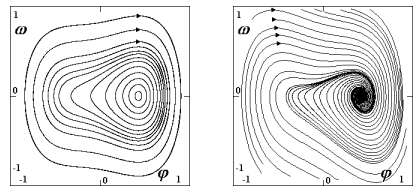
Fázový portrét A=0.22 N (F=2.28 N): postkritický stav (po vzniku druhého stabilního řešení)
Po vzniku druhého stabilního řešení (a také jednoho nestabilního řešení) se fázové portréty kvalitativně změnily, viz obr. 5. Portréty nyní obsahují dva soupeřící stabilní přitažlivé body (obě stabilní statická řešení) a nestabilní sedlový bod ležící mezi nimi (nestabilní řešení).
Z obr. 5 je vidět, že stabilní řešení "na straně imperfekce", tj. řešení, které existovalo i v prekritické oblasti, má větší přitažlivost (je stabilnější), než řešení nově vzniklé.
6. Chaotické chování
Jakmile na model aplikujeme v čase harmonicky proměnné zatížení (v našem případě sílu P) přestane být fáze budící síly 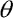 konstantní. Fázový prostor se tak stane třídimenzionální. Zároveň vznikne možnost existence složitějších druhů chování. Na obr. 6 je naznačen vývoj systému k tomuto stavu při vzrůstající velikosti amplitudy A, při kruhové frekvenci budící síly
konstantní. Fázový prostor se tak stane třídimenzionální. Zároveň vznikne možnost existence složitějších druhů chování. Na obr. 6 je naznačen vývoj systému k tomuto stavu při vzrůstající velikosti amplitudy A, při kruhové frekvenci budící síly  =2 rad.s-1 (0.318 Hz).
=2 rad.s-1 (0.318 Hz).
 | Obr. 6a: A=0.31 N (F=2.37 N): projekce jednoduchého limitního cyklu, v Poincarého mapě, pro kterou platí  =2 =2  s, s = 0, 1,..., má tento cyklus dva body (existuje ještě jednodušší cyklus s jedním bodem); s, s = 0, 1,..., má tento cyklus dva body (existuje ještě jednodušší cyklus s jedním bodem);
|
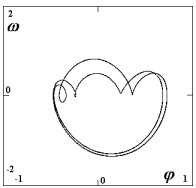 | Obr. 6b: A=0.32 N (F=2.38 N): projekce zdvojeného limitního cyklu, v Poincarého mapě má cyklus čtyři body; |
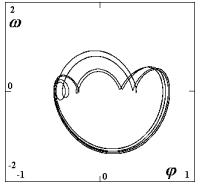 | Obr. 6c: A=0.325 N (F=2.385 N): další zdvojení; projekce dvakrát zdvojeného limitního cyklu, v Poincarého mapě má cyklus osm bodů; |
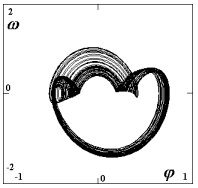 | Obr. 6d: A=0.33 N (F=2.39 N): zřejmě kvaziperiodické chování viz [3] (trajektorie je pro ilustraci omezená - trajektorie vyplňují souvislou oblast), v Poincarého mapě dvě souvislé oblasti; |
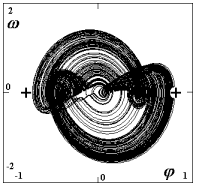 | Obr. 6e: A=0.35 N (F=2.41 N): chaos (trajektorie je pro ilustraci omezená), Poincarého mapa je fraktál, viz obr. 7 |
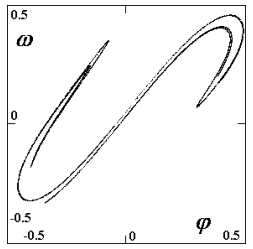 | Obr. 7: A=0.35 N (F=2.41 N): Poincarého mapa atraktoru na obr. 6e; poměrně řídká fraktální struktura, odhad Hausdorffovy dimenze dc=1.28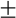 0.02 0.02
|
Fraktál vzniklý v Poincarého mapě na obr. 7 byl v přesnější reprezentaci podroben měření fraktální dimenze optimalizovanou metodou box-counting, viz [4]. Naměřená hodnota Hausdorffovy dimenze je dc=1.28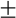 0.02. Histogram fraktálu byl také podroben fraktální analýze s naměřenou hodnotou informační dimenze di=1.21
0.02. Histogram fraktálu byl také podroben fraktální analýze s naměřenou hodnotou informační dimenze di=1.21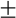 0.01.
0.01.
Zajímavostí ukázaného podivného atraktoru je, že extrémní výchylky statického řešení (viz obr. 2) jsou téměř shodné s extrémními výchylkami při pohybu na tomto atraktoru (viz obr. 6e). Jinak řečeno: Atraktor jen velmi málo překračuje výchylku při statickém zatížení odpovídající konstantní silou (rovnou amplitudě A), což je překvapivé.
7. Existence více limitních množin
Nelineární dynamický systém může být obohacen kromě chaotického chování také existencí více limitních cyklů. Myslíme tím, že máme-li systém se shodnými parametry, ale odlišnými počátečními podmínkami, může se stát, že se ustálí do navzájem různých limitních množin. Na obr. 8 jsou pro amplitudu A=0.4 N ukázány nalezené limitní množiny.
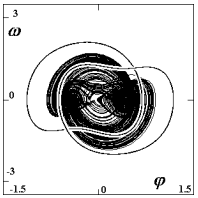 | Obr. 8: Schéma nalezených limitních množin pro amplitudu budící síly A=0.4 N (F=2.46 N). Podivný atraktor a dva jednoduché (při odhlédnutí od imperfekce antimetrické) jednobodové limitní cykly (v Poincarého mapě mají jeden bod). |
8. Závěr
Popsaný jednostupňový model se při své jednoduchosti v základních rysech shoduje se studovanou úlohou. Vykazuje ztrátu stability, vzniká zde druhé stabilní řešení a první řešení "na straně imperfekce" se správně ukazuje jako přitažlivější, přičemž rozdíl v přitahování se s rostoucí silou vyrovnává.
Nalezený chaotický stav pohybu vykazuje překvapivé vlastnosti a ukazuje, že tento stav může být pro konstrukci řešeného typu výhodnější, než jednodušší periodický druh pohybu (viz obr. 8).
Poděkování
Tento příspěvek je vytvořen v rámci výzkumného záměru CEZ: J22/98: 261100009 a s podporou grantu GA ČR 103/02/1030.
Reference
[1] Frantík P., Jednostupňový model vzpěru prutu, uveřejněno na internetu na adrese: http://kitnarfovo.misto.cz/pub/2002.02.onefreed/onefreed.htm, únor 2002
[2] Frantík P., Prut v oblastech velkých deformací: Řešení experimentu, IV. konferencia so zahraničnou účasťou: Staticko-konstrukčné a stavebno-fyzikálne problémy stavebných konštrukcií, Tatranská Lomnica, Vysoké Tatry, november 2002
[3] Macur J., Úvod do teorie dynamických systémů a jejich simulace, PC-DIR 1995, Brno 2002
[4] Frantík P., Macur J., Měření fraktální dimenze lomové plochy, seminář Problémy lomové mechaniky II, ÚFM Akademie věd ČR v Brně, Brno, červen 2001