Abstract
Experimental techniques for measurement of simple slender constructions undergo large deformations and also comparisons of experimental vs. numerical results are described in this paper.
Úvod
Výpočet konstrukcí ze štíhlých prutů zatížených tak, že dochází k velkým posunutím, je zejména při existenci nestabilit poměrně náročný a zasluhuje si pozornost z hlediska experimentálního ověření. Experimenty na takových konstrukcích jsou ale provázeny komplikacemi, jako například vliv vlastní tíhy (chceme-li ho eliminovat), nebo problémy se správnou realizací zatížení. Zde jsou ukázány postupy a výsledky experimentů na štíhlém ocelovém prutu konstantního průřezu, u kterého je předpokládáno fyzikálně lineární působení (poměrné přetvoření je lineárně závislé na napětí).
Výpočty
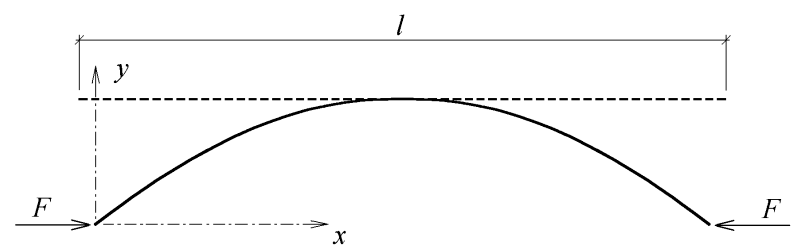
Uvažujme oprávněně, že u štíhlého prutu v případě rovinného ohybu lze zanedbat vliv normálových a posouvajících sil na posunutí bodů prutu. Vstupem do výpočtů, provedených metodou použitou v [1], srovnávaných s experimentálními výsledky, pak jsou dva parametry: délka prutu l a jeho ohybová tuhost EI. Ohybová tuhost je předem stanovena např. jednoduchou ohybovou zkouškou, nebo dynamickou zkouškou. Srovnání výsledků výpočtů s experimenty je provedeno na grafech s bezrozměrnými veličinami, takže hodnoty těchto parametrů nejsou důležité.
Experimenty a srovnání
Byly provedeny tři experimenty:
Znázorníme si a popíšeme konfiguraci experimentů a výsledky srovnáme s výpočty.
Konzolový nosník zatížený osamělým momentem
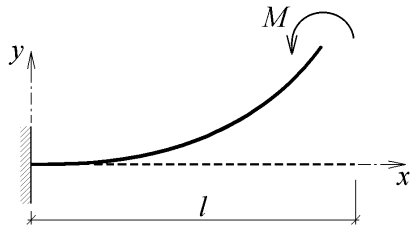
Úloha na obr. 1 má za daných předpokladů přesné řešení, ale experimentálně je ze všech tří úloh nejnáročnější. Je zde totiž problém vytvoření a nanesení osamělého momentu na konec konzoly. Dále je třeba eliminovat vliv vlastní tíhy. Vyřešení těchto potíží je znázorněno na obrázku 2.
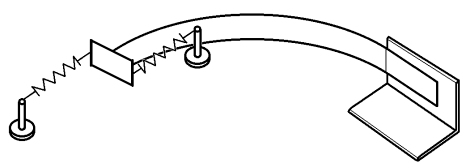
Vliv vlastní tíhy je eliminován horizontální polohou roviny ohybu a dostatečným rozdílem mezi šířkou a výškou průřezu nosníku. Osamělý moment je nanesen dvojicí pružin působících prostřednictvím kolmého plátu upevněného na konci konzoly.
Pro tento experiment musí platit následující podmínky: stejná napjatost obou pružin; totožný směr pružin; stejná vzdálenost uchycení pružin na příčný plát od střednice prutu; jelikož pružinami měříme vnášenou sílu, je třeba kompenzovat vliv jejich tíhy na vlastní napjatost. Z uvedených podmínek je zřejmé, že experiment probíhá postupným přibližováním. Pozice pružin musí být postupně měněny tak, aby byly dodrženy popsané podmínky.
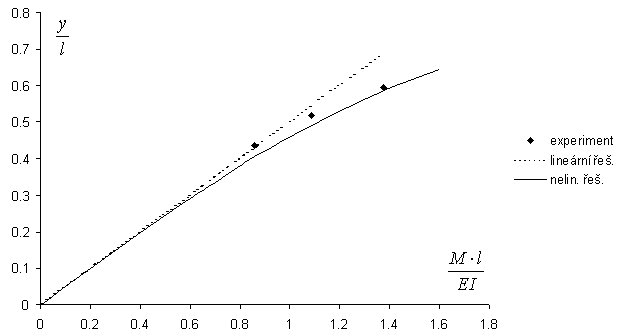
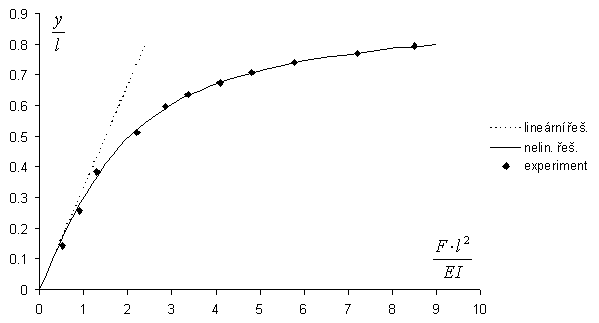
Na obrázku 3 je srovnání experimentu s výpočtem. Pro přehlednost je tam uvedeno i lineární řešení. Vzhledem k velké náročnosti experimentu byly změřeny pouze tři body, jak je patrno z obrázku 3.
Konzolový nosník zatížený osamělou silou
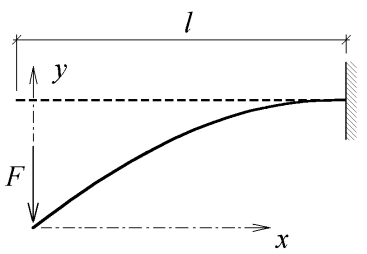
Úloha zobrazená na obrázku 4 je snadněji experimentálně řešitelná než úloha předchozí, avšak její výpočet je již komplikovanější. Experimentální řešení je na obrázku 5.
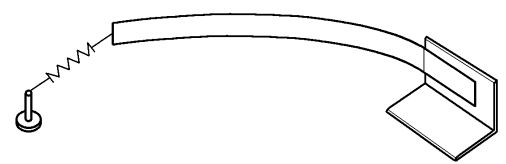
Experiment je proveden obdobně jako předchozí. Splněno musí být: pružina, kterou zároveň měříme vnášenou sílu má směr kolmý na tečnu prutu v místě uložení; pro odečet velikosti vnášené síly je třeba kompenzovat vlastní tíhu pružiny.
Vzpěr prutu
Úloha na obrázku 7 má jednu experimentální komplikaci a tou je stanovení velikostí tzv. imperfekcí (nedokonalostí ve smyslu přímosti prutu a konstantnosti tvaru a vlastností jeho průřezu). Tento problém bude ve výpočtu vyřešen sloučením možných imperfekcí do zvolené jediné. Velikost této imperfekce bude odhadnuta dle výsledků experimentu. Postup experimentu je znázorněn na obrázku 8.
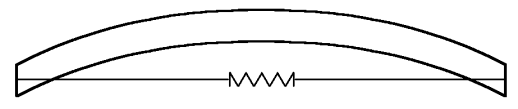
Tento experiment je také podobný předchozím. Upevnění prutu k podstavci může být provedeno uprostřed délky prutu svislými čelistmi.
Jelikož navzdory existenci imperfekcí existují stabilní řešení na obou stranách prutu (dle znázorněného postupu můžeme měřit vybočení "na stranu imperfekce" a také na stranu opačnou) je třeba vědět, kterou stranu měříme.
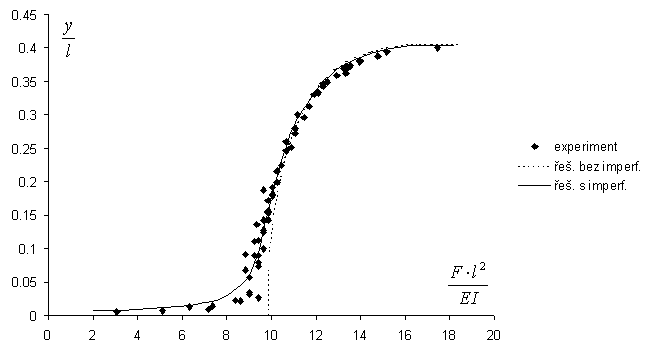
Závěr
Experimenty v oblasti velkých deformací mají velkou výhodu v tom, že je lze provádět za poměrně nenáročných podmínek (přesnost měřidel) a také důsledky zatěžování jsou dobře pouhým okem viditelné. Vyžadují však postupy, které nejsou obvyklé a kladou relativně velké požadavky na použitý materiál (pružnost materiálu).
Poděkování
Děkuji za finanční podporu výzkumnému záměru CEZ: J22/98: 261100009 a grantu GA ČR 103/97/K003.
Literatura
[1] Frantík, P.: Diskrétní řešení vzpěru prutu, seminář Problémy modelování, VŠB-TU Ostrava, leden 2002