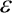 ) je minimální počet n-dimenzionálních krychlí velikosti
) je minimální počet n-dimenzionálních krychlí velikosti 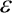 , nutných k pokrytí měřeného objektu nacházejícího se v n-dimenzionálním prostoru.
, nutných k pokrytí měřeného objektu nacházejícího se v n-dimenzionálním prostoru.
Abstract
Optimised box-counting method for estimation of capacitive fractal dimension is presented. Fractal dimensions of representation of fractured concrete surfaces are determined.
Keywords
Box-counting method, concrete, fractal dimension, fracture.
Úvod
Ve stavební praxi se používá mnoho charakteristik k popisu vlastností cementových kompozitů. Pro takovéto kvazikřehké materiály jako jsou beton, malta a cementová pasta je důležité, aby tyto charakteristiky byly v souladu s principy lomové mechaniky, viz např. Karihaloo (1995). Lomové plochy těchto kompozitů lze považovat za neregulární objekty - přírodní fraktály. Počátek rozvoje zkoumání fraktálních vlastností takových objektů je přisuzován Mandelbrotovi (1982). Charakteristikou, která popisuje vlastnosti takových objektů je fraktální dimenze.
Fraktální dimenze
Metoda, kterou použijeme ke stanovení fraktální dimenze se jmenuje box-counting. Tato metoda je založena na definici tzv. kapacitní dimenze. Kapacitní dimenze dc nějakého objektu je definována jako limita:
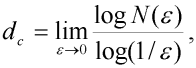
kde N(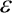 ) je minimální počet n-dimenzionálních krychlí velikosti
) je minimální počet n-dimenzionálních krychlí velikosti 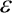 , nutných k pokrytí měřeného objektu nacházejícího se v n-dimenzionálním prostoru.
, nutných k pokrytí měřeného objektu nacházejícího se v n-dimenzionálním prostoru.
Metoda box-counting
Základní metodou pro odhad kapacitní dimenze je metoda box-counting (tuto metodu lze použít i na jiné zobecněné dimenze). Princip metody je takovýto: Pokryjeme měřený objekt krychlovými sítěmi Mi(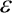 i), kde i=1, 2, ..., m a
i), kde i=1, 2, ..., m a 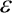 1 >
1 > 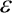 2 >... >
2 >... > 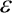 n je velikost krychlí v síti Mi. Pro každou síť stanovíme počet neprázdných krychlí Ni(
n je velikost krychlí v síti Mi. Pro každou síť stanovíme počet neprázdných krychlí Ni(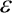 i). Odhad kapacitní dimenze je potom první (lineární) koeficient lineární aproximace bodů (log(1/
i). Odhad kapacitní dimenze je potom první (lineární) koeficient lineární aproximace bodů (log(1/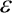 i), logNi(
i), logNi(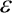 i)), i = 1, 2, ..., m. Je také dobré zároveň odhadnout chybu takto stanovené dimenze (výpočet je často značně nepřesný).
i)), i = 1, 2, ..., m. Je také dobré zároveň odhadnout chybu takto stanovené dimenze (výpočet je často značně nepřesný).
Optimalizovaná síť
V definici kapacitní dimenze je napsáno, že je třeba znát "minimální počet" krychlí. To je však problém optimalizace krychlové sítě. Optimalizaci je možno provést třeba tak, že síť rozdělíme na sloupce (řádky) a posouvat je horizontálně (vertikálně). Potom můžeme rozdělit sloupce (řádky) na jednotlivé krychle a tyto pak posouvat vertikálně (horizontálně).

Lomový experiment
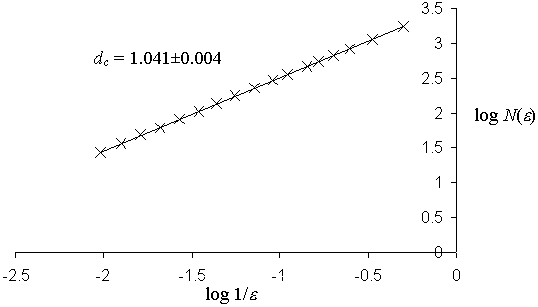
Provedeme-li lomový experiment, můžeme se snažit nalézt nějakou další invariantní charakteristiku. Mandelbrot ukázal, že řez lomovou plochou má stejné invariantní vlastnosti jako ona třídimenzionální lomová plocha. Řez lomovou plochou můžeme obdržet tak, že plochu ponoříme do barevného roztoku vhodných vlastností a výsledek vyfotíme. Z digitální fotky potom standardními grafickými prostředky získáme hranici mezi barvenými a nebarvenými částmi plochy. Na tuto hranici pak použijeme metodu pro stanovení fraktální dimenze


Závěr
Měřené hranice získané z experimentu jsou pouze mírně fraktální. Totiž od dimenze jedna se naměřené hodnoty příliš neliší. Nicméně stanovené odhady chyb naměřených hodnot nám dovolují říci, že lomová plocha je fraktál. Avšak abychom nalezli nějakou souvislost s materiálovými charakteristikami, bude potřeba provést mnohem více experimentů.
Poděkování
Autoři děkují za finanční podporu grantu č. 103/00/0603 z Grantové Agentury České Republiky a výzkumnému záměru reg. č. CEZ: J22/98: 261100009.
Literatura
Bažant, Z. P. (1995) Scaling of Quasi-Brittle Fracture and the Fractal Question. Journal of Engineering Materials and Technology, 117, 361 - 367.
Brandt, A. M., Prokopski, G. (1993) On the fractal dimension of fracture surfaces of concrete elements. Journal of Material Science, 28, 4762 - 4766.
Carpinteri, A., Chiaia, B., Invernizzi, S. (1999) Three-dimensional fractal analysis of concrete fracture at the meso-level. Theoretical and Applied Fracture Mechanics, 31, 163 - 172.
Carpinteri, A., Invernizzi, S. (2001) Uniaxial tensile test and fractal evaluation of softening damage in concrete. Fracture Mechanics of Concrete Structures, de Borst et al. (eds), Swets & Zeitlinger, Lisse, ISBN 90 2651 825 0, 19 - 25.
Karihaloo, B. L. (1995) Fracture mechanics of concrete. Longman Scientific & Technical, New York.
Mandelbrot, B.B. (1982) Fractal Geometry of Nature. Freeman, San Francisco.