Petr Frantík, Zbyněk Keršner, Jiří Macur
Abstract
Optimised box-counting method for estimation of capacitive fractal dimension is presented. Fractal dimensions of representation of fractured concrete surfaces are determined.
Key words: box-counting method, concrete, fractal dimension, fracture
1 Introduction
Many characteristics of cement based composites are used in civil engineering practise. Mechanical properties of quasi-brittle materials as concrete, mortar and cement paste are fully described using also fracture properties - see e.g. Karihaloo (1995). Fracture surfaces of these composites and also crack pattern are considered as irregular objects - natural fractals. The beginning of development of fractal characterisation of irregularity of these objects is related to work of e.g. Mandelbrot (1982). Many authors deal with fractal dimension/characterisation of fracture surfaces of concrete from the point of view of their determination and also correlation to others materials parameters, scaling aspects, etc. - e.g. Saouma et al. (1990), Brandt & Prokopski (1993), Bažant (1995), Carpinteri et al. (1999, 2001), Mechtcherine & Muller (2001). Optimised variant of box-counting method for estimation of capacitive fractal dimension is presented in the paper and the fractal dimensions of representation of fractured concrete surfaces of previously tested specimens are determined.
2 Fractal dimension
The box-counting method is based on fractal dimension that is called capacity. Capacity dc of any object is defined as the limit:
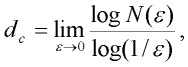| (1) |
where N(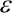
) is the minimal number of n-dimensional cubes of size 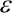, which are necessary for covering the measured object nested in n-dimensional space.
Box-counting method
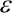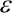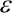Box-counting method is the basic method for numerical estimation of capacity (other generalized dimensions like informational dimension etc. can be applied as well but not so transparently). Let us cover measured object a number of cubic meshes Mi(i), where i = 1, 2, ..., n and 1 > 2 >... > 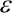n is size of cubes in mesh Mi. Then we must count the number of cubes Ni(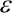i) for every mesh. Estimation of capacity is first coefficient of linear approximation of points (log(1/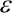i), logNi(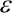i)), i = 1, 2, ..., n. The standard deviation of the measuring can be established by this method as well.
Mesh with optimalization
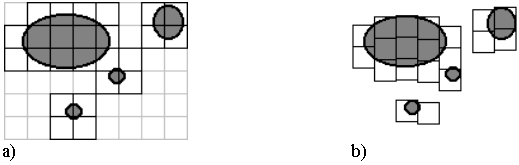
In definition of capacity is described "minimal number" of cubes - see Figure 1. It is the optimisation problem of mesh. We can divide a mesh to columns (rows) and slide them horizontally (vertically). Then the cubes in rows (columns) we can divide and slide them vertically (horizontally).
Comparison
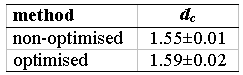
Let us compare non-optimised and optimised box-counting method applied to known fractal object. The fractal called Sierpinsky triangle is shown in Figure 2. Capacity of this fractal is 1.585. At equivalent conditions were estimated these values of capacity - see Table 1.
Table 1 Fractal dimension
3 Fracture experiment
In case of fracture experiment we try to find another invariant surface attribute. As Mandelbrot showed we suppose that the capacity of the one-dimensional planar section of the fracture surface has the same invariant properties as the full three-dimensional surface. We can obtain requested section if we immerge the surface to the coloured solution and take a digital photograph. The visualization of the boundary between the coloured (immerged) and non-coloured parts can be obtain by the help of standard image processing. An example of representation of fracture surface of specimen and its estimated capacity from linear approximatin of measured points is presented in Figure 3; all results are placed in Table 2.
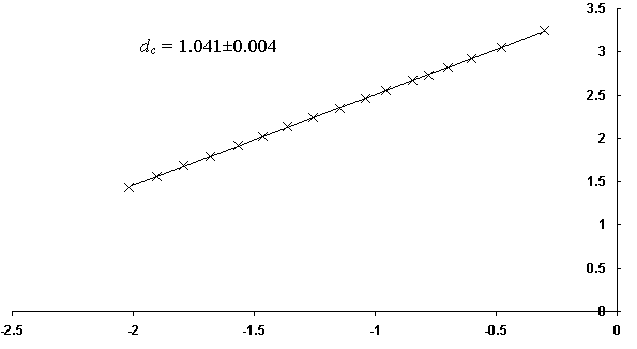
Table 2 Fractal dimensions
4 Conclusions
Measured boundary has weak fractal properties. However experiments showed that this facility is not the consequence of discretization error and we can assume that fracture surface is fractal. To determinate the correlation between the capacity of measured boundary and material attributes much more experiments need to be accomplished.
Acknowledgements
The authors thank for funding under grant No. 103// from the Grant Agency of the Czech Republic and under the research project reg. No. CEZ: J22/98: 261100009.
References
Bažant, Z. P. (1995) Scaling of Quasi-Brittle Fracture and the Fractal Question, Journal of Engineering Materials and Technology, 117, 361-367.
Brandt, A. M., Prokopski, G. (1993) On the fractal dimension of fracture surfaces of concrete elements. Journal of Material Science, 28, 4762 - 4766.
Carpinteri, A., Chiaia, B., Invernizzi, S. (1999) Three-dimensional fractal analysis of concrete fracture at the meso-level. Theoretical and Applied Fracture Mechanics, 31, 163 - 172.
Carpinteri, A., Invernizzi, S. (2001) Uniaxial tensile test and fractal evaluation of softening damage in concrete. Fracture Mechanics of Concrete Structures, de Borst et al. (eds), Swets & Zeitlinger, Lisse, ISBN 90 2651 825 0, 19 - 25.
Karihaloo, B. L. (1995) Fracture mechanics of concrete. Longman Scientific & Technical, New York.
Mandelbrot, B.B. (1982) Fractal Geometry of Nature. Freeman, San Francisco.
Mechtcherine, V., Muller, H. S. (2001) Fractological investigation on the fracture in concrete. Fracture Mechanics of Concrete Structures, de Borst et al. (eds), Swets & Zeitlinger, Lisse, ISBN 90 2651 825 0, 81 - 88.
Saouma, V. E., Barton, C. C., Gamaleldin, N. A. (1990) Fractal characterization of fracture surfaces in concrete. Engineering Fracture Mechanics, 35, No. 1/2/3, 47 - 53.
Petr Frantík, Brno University of Technology, Civil Engineering Faculty, Institute of Structural Mechanics, Veveří 95, 662 37 Brno, Czech Republic, e-mail: kitnarf
centrum.cz
Dr. Zbyněk Keršner, Brno University of Technology, Civil Engineering Faculty, Institute of Structural Mechanics, Veveří 95, 662 37 Brno, Czech Republic, e-mail: kersner.z@fce.vutbr.cz
Jiří Macur, Assoc. Prof., Brno University of Technology, Civil Engineering Faculty, Institute of , Veveří 95, 662 37 Brno, Czech Republic, e-mail: macur.j@fce.vutbr.cz