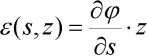
Abstract
Approximate continuous nonlinear solution of the beam buckling is described in this paper. The solution is verified by experimental results and results of different nonlinear solutions. The presented solution is in good line with these results.
Úvod
Budeme-li se zabývat vzpěrem štíhlých prutů z fyzikálně lineárního materiálu v oblastech pokritického působení (po ztrátě stability), nemůžeme pominout nelineární charakter takové úlohy. Dopad různých zjednodušení je u této úlohy obvykle výrazný. Uvedeme zde proto i experimentální výsledky.
Předpoklady pro odvození nelineárního řešení
Předpokládejme, stejně jako u lineárního řešení, že štíhlý prut lze zjednodušit na jednodimenzionální útvar, kde platí předpoklad o zachování rovinnosti průřezů po deformaci (Bernoulli-Navierova hypotéza). Také nechť je tento prut z fyzikálně lineárního materiálu, tj. vztah mezi napětím a poměrným přetvořením je lineární (Hookeův zákon). A pro jednoduchost zanedbejme účinky normálových a posouvajících sil na deformaci prutu. Rozdílem od lineárního odvození bude zpřesnění vztahu pro poměrné přetvoření v závislosti na deformaci prutu. Definujme jej takto [1]:
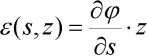| (1) |
kde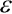 
je poměrné přetvoření vláken ve vzdálenosti z od těžiště průřezu se souřadnicí s měřenou po střednici prutu od zvoleného počátku a 
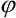je funkce pootočení průřezu.
Tento výraz vyjadřuje přesněji závislost mezi křivostí prutu a jeho přetvořením od ohybového momentu s tím, že poměrné přetvoření uvažujeme na deformovaném tvaru prutu. Tento vztah nám natolik zkomplikuje úlohu, že ji vyřešíme pouze přibližně.
Řešení Ritzovou metodou
K základním metodám pro přibližná řešení úloh patří Ritzova metoda, kterou zde s výhodou použijeme. Tato metoda užívá energetických principů a je vhodná pro hledání přibližných řešení, pokud máme k dispozici vhodné aproximační funkce. Mějme úlohu hledání vzepětí přímého prutu konstantního průřezu oboustranně kloubově uloženého. Předpokládejme, že výsledný deformovaný tvar bude symetrický. Z titulu symetrie uvažujme polovinu prutu (viz obr. 1) a označme l =L/2, kde L je délka prutu.
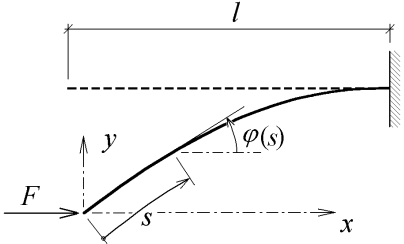
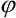(s) je pootočení obecného průřezu se souřadnicí s měřenou po střednici prutu.
Nyní je třeba zvolit vhodnou aproximační funkci pootočení průřezu. Protože nám jde o nalezení jednoduchého explicitního vztahu pro deformaci prutu, použijeme funkci s pouze jedním neznámým parametrem v tomto tvaru:
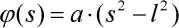 | (2) |
kde a je hledaný neznámý parametr. Pro jeho nalezení užijeme právě Ritzovu metodu. Nejprve formulujme výraz pro potenciální energii deformace vnitřních sil:
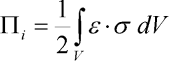 | (3) |
kde V je objem tělesa, 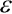je poměrné přetvoření elementu objemu dV a 
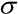je napětí příslušné poměrnému přetvoření 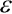. Tento vztah lze za výše uvedených předpokladů přepsat na:
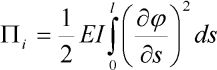 | (4) |
kde EI je ohybová tuhost prutu. Po dosazení aproximace (2) a po provedení integrace dostáváme:
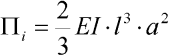 | (5) |
což je hledaný výraz. Dále potřebujeme formulovat výraz pro potenciální energii deformace vnějších sil, v našem případě:
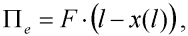 | (6) |
kde x(l) je vodorovná souřadnice vetknutí vzhledem ke koncovému bodu, viz obr. 1. Vodorovnou souřadnici x obecného bodu deformovaného tvaru poloviny prutu definujme takto:
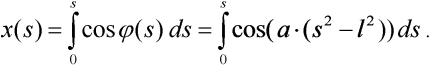 | (7) |
Tento integrál vyřešíme pouze přibližně s užitím prvních tří členů Taylorova rozvoje funkce cos x:
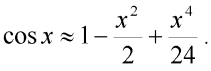 | (8) |
Po dosazení do (7) obdržíme:
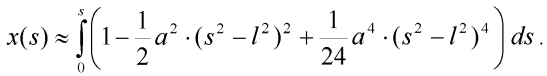 | (9) |
Provedeme integraci a dostáváme přibližný výraz pro hledanou souřadnici obecného bodu uvažované poloviny prutu:
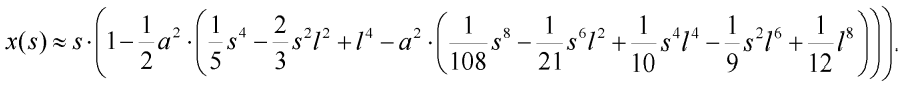 | (10) |
Dosazením do výrazu (6) obdržíme konečný vztah pro potenciální energii deformace vnějších sil:
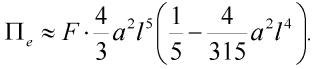 | (11) |
Sestavíme celkovou potenciální energii deformace systému:
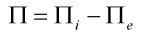 | (12) |
Po dosazení (5) a (11) dostaneme:
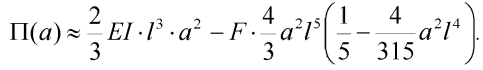 | (13) |
Pro stabilní řešení úlohy platí, že celková potenciální energie deformace systému musí nabývat svého minima (lokálního minima) a tedy v našem případě musí být alespoň splněna podmínka:
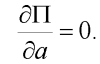 | (14) |
Po dosazení výrazu (13) obdržíme rovnici:
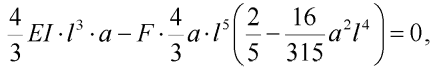 | (15) |
která má triviální řešení a1 = 0 a dále nenulová řešení ve tvaru:
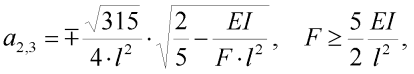 | (16) |
Pro úplnost uveďme přibližný vztah pro souřadnici y obecného bodu deformovaného tvaru poloviny prutu:
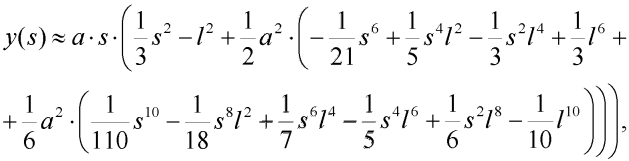 | (17) |
a také přibližný výraz pro vzepětí prutu:
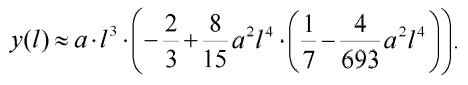 | (18) |
Vybraná řešení a experiment
Experiment byl proveden na štíhlém ocelovém prutu v pokritické oblasti vzpěrné síly, kde imperfekce prutu nemá velký význam. Výsledky byly dále srovnány se spojitým řešením dle Ržanicyna [1], diskrétním jednostupňovým řešením [2], diskrétní metodou pro geometricky nelineární výpočty prutových konstrukcí [3] a upraveným klasickým řešením zanedbávajícím přesný vztah pro křivost prutu [4].
Vzepětí jednostupňového modelu prutu [2] je při splnění počáteční tuhosti modelu vzhledem k lineárnímu řešení dáno implicitní rovnicí:
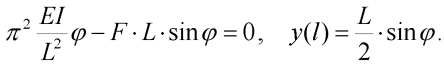 | (19) |
Přibližným netriviálním řešením této rovnice je výraz:
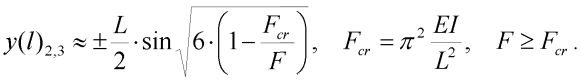 | (20) |
Diskrétní vícestupňové řešení [3] se shoduje s Ržanicynovým řešením [1] natolik, že nemá smysl je odděleně uvádět. Vzhledem k jejich shodě a k faktu, že jsou tato řešení založena na jiných přístupech je lze shodně označovat za přesné řešení.
Řešení [4] vychází z klasického řešení vzpěru přímého prutu (předpokládá se vybočení ve tvaru jedné sinové půlvlny) ze statických podmínek rovnováhy, ale nezanedbává vliv sblížení konců prutu. Pro stabilní netriviální řešení vyplývá pro vzepětí prutu výraz:
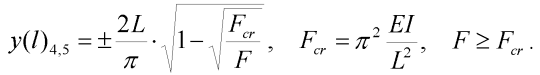 | (21) |
Srovnání
Abychom zhodnotili význam prezentovaného řešení, provedeme srovnání. Budeme vycházet z parametrů experimentálního prutu L=0.723 m (l=0.3615 m), EI=0.1149 Pa.m4.
Kritická síla prutu Fcr je dle vzorců (19) a (20) přibližně 2.17 N, což představuje její přesnou hodnotu. Odvozené řešení dává hodnotu přibližně 2.20 N, viz (16). Rozdíl tedy činí méně než 2%.
Podívejme se na graf závislostí vzepětí prutu na velikosti vzpěrné síly F (viz obr. 2) a také na deformované tvary odvozeného řešení, přesného řešení [3] a experimentu (viz obr. 3).
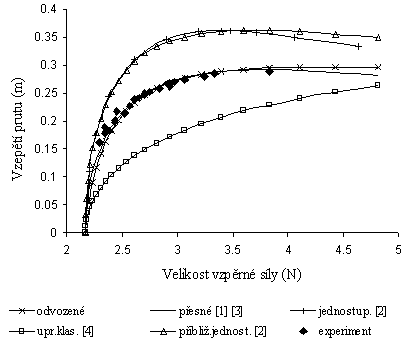
Obr. 2: Srovnání závislostí vzepětí prutu na velikosti vzpěrné síly
Obr. 3: Srovnání deformovaných tvarů pro vzpěrnou sílu F=3.5 N
Z grafu na obr. 2 je patrné, že řešení jednostupňového modelu [2] dává pro funkci vzepětí dobrou představu o přesném řešení. Naopak upravené klasické řešení [4] zanedbávající přesný vztah pro křivost příliž neuspělo. Je to značně způsobeno také volbou nevhodné průhybové funkce. Nicméně i toto řešení je v oblasti kritické síly dobrou aproximací.
Odchylka hodnoty vzepětí mezi přesným řešením a odvozeným řešením je menší než 2% až do velikosti vzpěrné síly F=4 N. Hůře vyznívá srovnání deformovaných tvarů pro sílu F=3.5 N, viz obr. 3. Určit míru chyby řešení se ukazuje u pokritického vzpěru jako komplikovaný problém, který je určován náročností úlohy (oblast ztráty a následné obnovení stability prutu).
Experimentální výsledky přesvědčivě ukazují, že obě řešení [1] a [3] jsou zřejmě oprávněně považovaná za přesná.
Závěr
Prezentované odvození spojitého řešení vzpěru přímého prutu poměrně dobře uspělo ve srovnání s řešeními [1] a [3], považovanými za přesná. Provedený experiment taktéž prokázal, vhodnost označení řešení [1] a [3] za přesná. Prezentovaný jednostupňový model [2] se ukazuje jako dobrá a vzhledem k náročnosti jednoduchá sonda vlastností studovaného problému. I taková primitivní náhrada spojitého řešení vykazuje obdobné vlastnosti jako řešení [1] a [3]. Řešení [4] lze považovat za přesné pouze v intervalu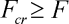 
. Pro sílu F větší než Fcr je pouze topologicky správné, nicméně hodnotami a deformovaným tvarem špatné.
Poděkování
Příspěvek byl zpracován za podpory výzkumného záměru reg. č. CEZ J22/98:261100009.
Literatura
1. Ržanicyn, A. R. Ustojčivosť ravnovesija uprugich system, Gosudarstvenoje izdatělstvo techniko-teoretičeskoj literatury Moskva 1955.
2. Frantík, P. Jednostupňový model vzpěru prutu, http://kitnarfovo.misto.cz/pub/2002.02.onefreed/onefreed.htm, únor 2002.
3. Frantík, P. Diskrétní řešení vzpěru prutu, sborník Problémy modelování (X. komorní seminář Úskalí lom. mechniky cem. kompozitů), VŠB-TU Ostrava a VUT v Brně, leden 2002.
4. Frantík, P. K problematice vzpěru a k zjednodušením lineární mechaniky, III. komorní seminář Úskalí lom. mechniky cem. kompozitů, VUT v Brně, http://www.fce.vutbr.cz/stm/fracture/kseminar/ks03/zprava.htm, listopad 2001.