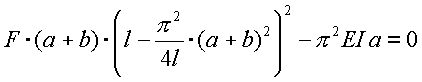
Newtonova iterační metoda pro parametrické řešení rovnice vzpěru
Petr Frantík
Úvod
Newtonova iterační metoda se používá pro řešení jedné reálné rovnice o jedné reálné proměnné. Použijeme ji obvykle tehdy, neznáme-li explicitní vyjádření řešení této rovnice. Tuto rovnici lze psát ve tvaru:
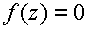
kde všechna z vyhovující této rovnici (řešení rovnice), nazýváme kořeny rovnice. Newtonova metoda je jednou z numerických metod pro nalezení přibližného řešení. Její iterační předpis vypadá takto:
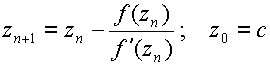
kde c je počáteční hodnota, či počáteční bod iterace. Tímto bodem je určen postup newtonovy metody. Z jednoho počátečního bodu lze proto nalézt pouze jeden kořen rovnice. Každému kořenu rovnice tak přísluší určitá množina počátečních hodnot, které povedou k nalezení tohoto kořene.
Rovnice vzpěru
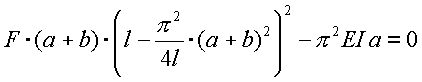
Výpočty
Pro zobrazení vlastností Newtonovy metody bude nejlepší, zobrazíme-li si komplexní rovinu počátečních bodů a každý bod označíme vybranou barvou příslušnou ke kořenu, ke kterému Newtonova metoda konverguje pro daný počáteční bod. Navíc bude dobré, rozlišíme-li počet iterací, nutných k dosažení zvolené přesnosti.
Na obrázcích 2 a 4 intenzita barvy odpovídá počtu iterací. Černá barva odpovídá případu, kdy metoda nezkonvergovala pro daný maximální počet iterací (v těchto oblastech se metoda chová chaoticky, viz bifurkační diagram). Čím menší počet nutných iterací, tím tmavší je daná barva. Dosáhne-li počet iterací hodnoty, kdy je intenzita barvy maximální, tak se intenzita barvy se dále nezvyšuje.

Obr. 1: Nalezená řešení (na vodorovné ose síla, na svislé vzepětí prutu)

Obr. 2: Odpovídající bazény přitažlivosti Newtonovy metody
Detail fraktální oblasti

Obr. 3: Zvětšení oblasti s bodem bifurkace Fbif=97.517526 N, abif=-0.068 m

Obr. 4: Odpovídající bazény přitažlivosti Newtonovy metody
Závěr