Abstract
The approximate continuous nonlinear solution of cantilever beam deflection is described. The solution is verified by results of other discrete nonlinear methods. The solution is in good line with these results.
Úvod
If we will deal with slender beams from physically linear material with large deformation problems, we cannot vanish nonlinearities. We will show here on example of simple construction its special nonlinear analytic solution and comparison with other nonlinear soulutions.
Předpoklady pro odvození nelineárního řešení
Předpokládejme, stejně jako u lineárního řešení, že štíhlý prut lze zjednodušit na jednodimenzionální útvar, kde platí předpoklad o zachování rovinnosti průřezů po deformaci (Bernoulli-Navierova hypotéza). Také nechť je tento prut z fyzikálně lineárního materiálu, tj. vztah mezi napětím a poměrným přetvořením je lineární (Hookeův zákon). A pro jednoduchost zanedbejme účinky normálových a posouvajících sil na deformaci prutu. Rozdílem od lineárního odvození bude zpřesnění vztahu pro poměrné přetvoření v závislosti na deformaci prutu. Definujme jej takto [1]:
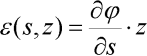 | (1) |
kde 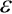 je poměrné přetvoření vláken ve vzdálenosti z od těžiště průřezu se souřadnicí s měřenou po střednici prutu od zvoleného počátku a
je poměrné přetvoření vláken ve vzdálenosti z od těžiště průřezu se souřadnicí s měřenou po střednici prutu od zvoleného počátku a 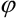 je funkce pootočení průřezu. Tento výraz vyjadřuje přesněji závislost mezi křivostí prutu a jeho přetvořením od ohybového momentu s tím, že poměrné přetvoření uvažujeme na deformovaném tvaru prutu. Tento vztah nám natolik zkomplikuje úlohu, že pro řešení použijeme pouze přibližnou metodu.
je funkce pootočení průřezu. Tento výraz vyjadřuje přesněji závislost mezi křivostí prutu a jeho přetvořením od ohybového momentu s tím, že poměrné přetvoření uvažujeme na deformovaném tvaru prutu. Tento vztah nám natolik zkomplikuje úlohu, že pro řešení použijeme pouze přibližnou metodu.
Řešení Ritzovou metodou
K základním metodám pro přibližná řešení úloh patří Ritzova metoda, kterou zde s výhodou použijeme. Tato metoda užívá energetických principů a je vhodná pro hledání přibližných řešení, pokud máme k dispozici vhodné aproximační funkce. Mějme úlohu hledání průhybu konzoly z přímého prutu konstantního průřezu od osamělé síly, viz obr. 1.
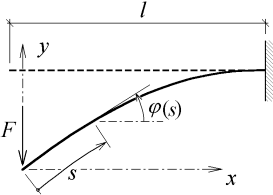
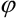 (s) je pootočení obecného průřezu se souřadnicí s měřenou po střednici prutu.
(s) je pootočení obecného průřezu se souřadnicí s měřenou po střednici prutu.
Nyní je třeba zvolit vhodnou aproximační funkci pootočení průřezu. Protože nám jde o nalezení jednoduchého explicitního vztahu pro deformaci prutu, použijeme funkci s pouze jedním neznámým parametrem v tomto tvaru:
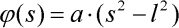 | (2) |
kde a je hledaný neznámý parametr. Pro jeho nalezení užijeme právě Ritzovu metodu. Nejprve formulujme výraz pro potenciální energii deformace vnitřních sil:
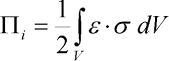 | (3) |
kde V je objem tělesa, 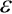 je poměrné přetvoření elementu objemu dV a
je poměrné přetvoření elementu objemu dV a 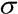 je napětí příslušné poměrnému přetvoření
je napětí příslušné poměrnému přetvoření 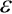 . Tento vztah lze za výše uvedených předpokladů přepsat na:
. Tento vztah lze za výše uvedených předpokladů přepsat na:
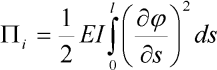 | (4) |
kde EI je ohybová tuhost prutu. Po dosazení aproximace (2) a po provedení integrace dostáváme:
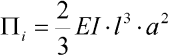 | (5) |
což je hledaný výraz. Dále potřebujeme formulovat výraz pro potenciální energii deformace vnějších sil, v našem případě:
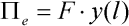 | (6) |
kde y(l) je svislá souřadnice vetknutí vzhledem ke koncovému bodu, viz obr. 1. Svislou souřadnici deformovaného tvaru obecného bodu y(s) definujme takto:
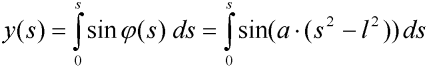 | (7) |
Tento integrál vyřešíme pouze přibližně s užitím prvních dvou členů Taylorova rozvoje funkce sin x:
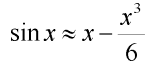 | (8) |
Po dosazení do (7) obdržíme:
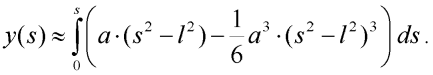 | (9) |
Provedeme integraci a dostáváme přibližný výraz pro hledanou souřadnici bodu prutu:
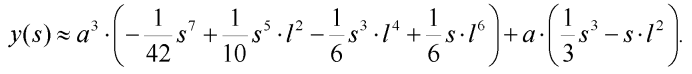 | (10) |
Dosazením do výrazu (6) obdržíme konečný vztah pro potenciální energii deformace vnějších sil:
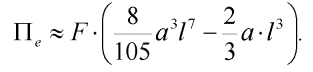 | (11) |
Sestavíme celkovou potenciální energii deformace systému:
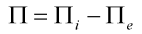 | (12) |
Po dosazení (5) a (11) dostaneme:
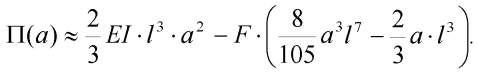 | (13) |
Pro stabilní řešení úlohy platí, že celková potenciální energie deformace systému musí nabývat svého minima (lokálního minima) a tedy v našem případě musí být alespoň splněna podmínka:
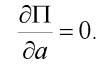 | (14) |
Po dosazení výrazu (13) obdržíme rovnici:
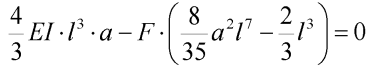 | (15) |
která má řešení ve tvaru:
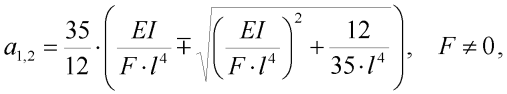 | (16) |
kde kořen a1 je parametr hledaného prvního stabilního řešení (uvádíme zde přívlastek "první stabilní", protože existuje nejméně jedno další stabilní řešení úlohy, nalezené pomocí metody [2]). Pro sílu F=0 je kořen a1 nulový. Kořen a2 je přiblížení k prvnímu nestabilnímu řešení úlohy (potenciální energie deformace systému zde nabývá svého lokálního maxima) a nebudeme se jím dále zabývat.
Pro úplnost uveďme přibližný vztah pro souřadnici x obecného bodu deformovaného tvaru prutu:
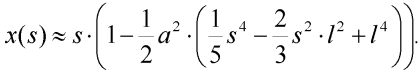 | (17) |
Srovnání řešení
Abychom zhodnotili význam prezentovaného řešení, srovnáme jej s výsledky několika jiných vybraných řešení (experiment na skutečné konstrukci prozatím nebyl proveden). Úloha byla řešena náhradou jednostupňovým modelem [3], dále diskrétní metodou pro geometricky nelineární výpočty prutových konstrukcí [2] a dále geometricky nelineárním prutovým modelem MKP.
Přibližným řešením svislé deformace koncového bodu y jednostupňového modelu [3] je při splnění počáteční tuhosti modelu vzhledem k lineárnímu řešení rovnice:
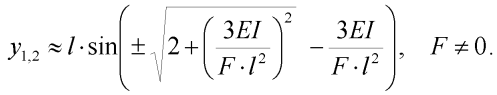 | (18) |
Obdobně jako u rovnice (16) je hodnota y1 hledanou svislou deformací a také pro sílu F=0 je hodnota y1=0. Diskrétní vícestupňová řešení obou zmíněných metod se shodují natolik (rozdíl maximálně 0.1%), že není třeba uvádět obojí. Tato řešení souhrnně popíšeme jako diskrétní vícestupňová. Z úsporných důvodů si ukážeme grafy všech vybraných řešení pouze pro koncovou svislou deformaci konzoly v závislosti na velikosti síly F. Grafy jsou společně zobrazeny na obr. 2.
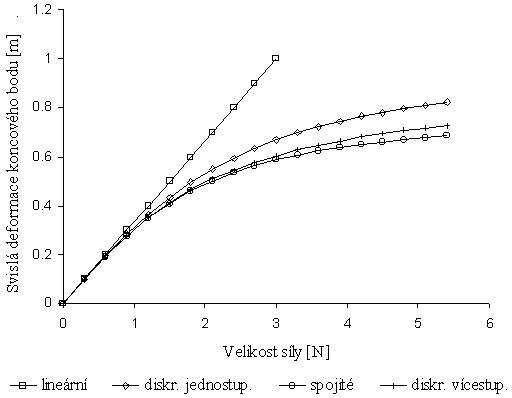
Rozdíl mezi diskrétním vícestupňovým řešením a odvozeným řešením je pro koncovou svislou deformaci menší než 3% až do velikosti deformace 0.6 metru (prut délky 1 metr).
Závěr
Ačkoliv nebyl proveden experiment na skutečné konstrukci, shoda dvou nezávislých diskrétních metod založených na odlišném přístupu dává dobré hodnocení pro odvozené řešení. Jak je patrné z grafů na obr. 2, řešení je dobrou aproximací i pro velké svislé výchylky.
Poděkování
Příspěvek byl zpracován za podpory výzkumného záměru reg. č. CEZ J22/98:261100009.
Literatura
1. Ržanicyn, A. R. Ustojčivosť ravnovesija uprugich system, Gosudarstvenoje izdatělstvo techniko-teoretičeskoj literatury, Moskva 1955.
2. Frantík, P. Diskrétní řešení vzpěru prutu, sborník Problémy modelování (X. komorní seminář Úskalí lom. mechniky cem. kompozitů), VŠB-TU Ostrava a VUT v Brně, leden 2002.
3. Frantík, P. Sledování a simulace nelineární dynamické konstrukce, sborník 3. odborného semináře dok. studia, VUT v Brně, únor 2001.