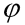Diskrétní řešení vzpěru prutu

Discrete solution of beam buckling

Petr Frantík

Abstract

Here is described discrete method for solution of beam buckling. The beam is divided into a number of tough elements. There is a joint with rotary spring between the elements. This discrete model is represented by system of nonlinear algebraic equations. The Newton's iterative method is used for solution of these equations.

Úvod

Pokud budeme uvažovat základní způsoby namáhání (tah, tlak, ohyb, apod.) a budeme-li tato namáhání aplikovat na štíhlé pruty, potom v případě tlaku zjistíme potíže. Štíhlý prut bude vybočovat a tím přestane být jeho stav "jednoduchý". Takovému chování říkáme vzpěr.

Vzpěr prutu

Pod pojmem vzpěru prutu mysleme stav prutu dle obrázku 1.

Prutem budeme uvažovat po své délce neproměnný, přímý jednodimenzionální útvar, jenž je ke své ose dokonale symetrický, jinak řečeno dokonale přímý a z dokonalého materiálu (bez poruch, nehomogenit). Jednoduše řečeno budeme řešit vzpěr přímého prutu.

Diskrétní řešení

Diskretizaci ve smyslu hledání posunutí pro konečný počet bodů prutu provedeme jednoduchým způsobem. Rozdělíme prut na určitý počet stejně dlouhých, tuhých (nedeformovatelných) částí (nazývejme je elementy), které jsou vzájemně spojeny kloubem s rotační pružinou, viz obrázek 2.

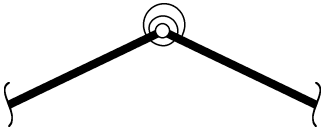
Pružina nechť vytváří moment přímo úměrný vzájemnému pootočení daných elementů. Tuto volbu můžeme vyjádřit rovnicí:

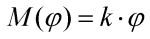
kde M je velikost momentu, kterým pružina na oba elementy působí, 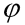je vzájené pootočení elementů, k nechť je konstanta, kterou zvolíme takto:

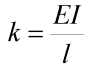
kde l je délka elementu a EI je ohybová tuhost prutu. Po diskretizaci může výpočetní model v obecnější poloze vypadat jako na obrázku 3.

Rovnice

Pro řešení zvolené úlohy můžeme použít dva postupy. Buď sestavíme statické podmínky rovnováhy, nebo využijeme obecnějšího energetického principu. Oba postupy, při správných podmínkách, dávají stejné výsledky (v takovém případě musí jít pro danou matematickou úlohu o přesné řešení). Zde použijeme pouze statických podmínek, protože nám to výrazně zkrátí zápis. Nicméně lze snadno dokázat, že oba postupy vedou ke stejným rovnicím.

Abychom mohli sestavit rovnice, musíme vše potřebné řádně označit, viz obrázek 4.

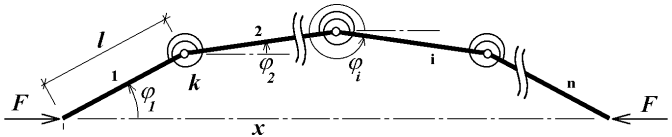
Na obrázku 4 je označeno vše co potřebujeme k odvození rovnic. Osa x je zvolena tak, že prochází oběma konci prutu a její počátek je zvolen v levém krajním konci. Dvojice sil F působí proti sobě na opačných koncích modelu ve směru osy x. Prut je rozdělen na n elemetů. Každý element označený od počátku indexy i=1,2,...,n je obecně pootočen o úhel 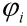a má vždy stejnou délku l. Každá pružina má vždy stejnou konstantu k. Pro celkovou délku modelu prutu L platí:

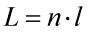
Pružiny rozlišujme podle toho, které elementy spojují. Pružina mezi elementy i a i+1 ponese index i,i+1. Moment pružiny i,i+1 označme M_i,i+1 a definujme jej takto:

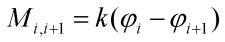
Element i v obecné poloze po vyjmutí je vidět na obrázku 5.

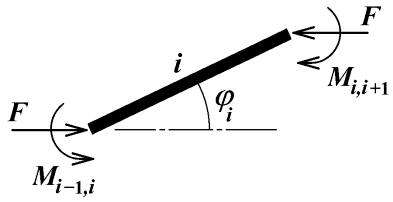
Sestavíme-li momentovou podmínku například k pravému konci elementu, vyjde nám:

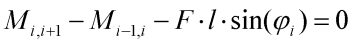
přičemž i=1,2,...,n a M_0,1=0, M_n,n+1=0. Po dosazení za momenty M a úpravě obdržíme pro i=1:

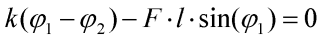
dále pro i=2,3,...,n-1:

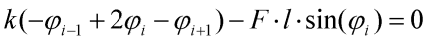
a nakonec pro i=n:

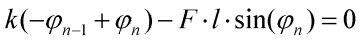
Dostáváme tedy soustavu n nelineárních algebraických rovnic pro n neznámých pootočení 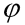. Tato soustava obecně nemá jediné řešení, což je v souladu s charakterem úlohy.

Řešení této soustavy rovnic musí navíc splňovat dvě podmínky. Obecně, a to i v případě, že bychom uvažovali prut obecného průřezu, musí hodnota pootočení 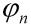vyjít právě taková, aby koncový bod polygonu elementů i=1,2,...,n ležel opět na ose x. Výpočet pootočení 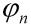je tedy v jistém smyslu nadbytečný (lze to považovat za dobrou kontrolu numerických výsledků). Symetrie popřípadě antisymetrie vzhledem k ose kolmé k prutu a jdoucí jeho středem je druhou, ovšem méně obecnou podmínkou.

Výpočet

Pro řešení výše uvedené soustavy rovnic byla použita Newtonova iterační metoda. Jelikož je tato metoda obecně známa, nebude zde více popisována.

Abychom mohli numericky řešit uvedenou soustavu rovnic, musíme vzít konkrétní prut. Zvolíme prut s těmito parametry: délka prutu L=1 m, ohybová tuhost EI=1 Pa.m4. Pro kritickou sílu platí:

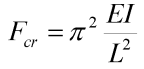
Dle zvolených parametrů je její hodnota F_cr=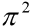, což je přibližně 9.87 N. Ještě před tím, než si ukážeme konkrétní řešení zvoleného prutu pomocí zde popsané metody, je třeba uvést vliv počtu elementů na přesnost řešení. Testy bylo prokázáno, že vypočtené hodnoty v závislosti na počtu elementů poměrně rychle konvergují. Dobré výsledky je možno dostat již pro 10 elementů. Rychlost konvergence je významě závislá na tom, jak blízko je zvolená síla blízko síle kritické.

Na obrázku 6 je vidět graf závislosti vzepětí prutu na síle F.

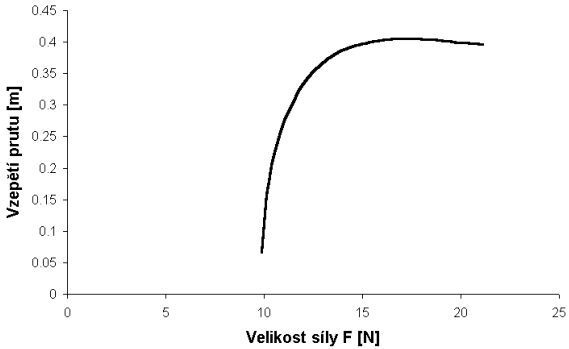
Na obrázku 6 jsou vidět hodnoty řešení, které je jedním ze dvou symetrických stabilních řešení pro vybočený prut. Z obrázku je vidět, že kritická síla z řešení touto metodou je v dobré shodě s výše vypočtenou hodnotou.

Závěr

Lze říci, že uvedená metoda pro řešení vzpěru prutu je dobrou alternativou analytickým řešením, nebo řešením jinými dikrétními metodami. Další verifikace výsledků jsou již mimo rámec tohoto příspěvku.

Poděkování

Práce na tomto příspěvku byla podporována z výzkumného záměru reg. č. CEZ J22/98:261100009.