Petr Frantík

Předmluva

Jedním z nástrojů popisu dynamického systému je poměrně obtížně numericky zvládnutelný výpočet spektra Ljapunovových exponentů. Problémy s hledáním této charakteristiky jsou však vyváženy informacemi, které nalezením spektra získáme. Ljapunovovy exponenty nám totiž přímo svými hodnotami říkají, jak se systém chová. Klasifikace chování se jinými způsoby provádí obtížněji (u systému, jenž studuji, jsem bez znalosti spektra Ljapunovových exponentů prováděl klasifikaci prostým pozorování vývoje projekce trajektorie). Myslím, že jedině s pomocí Ljapunovových exponentů, či podobného matematického nástroje, lze v rámci tolerancí jednoznačně rozhodnout o charakteru chování systému.

Úvod

Při této své práci jsem vycházel z [Viktor Votruba, diplomová práce, MU v Brně, Brno 2000].

Výpočet Ljapunovova spektra lze shrnout do několika zásadních bodů:

• Na určitém úseku řešíme soustavu nelineárních rovnic a s ní spjatou trojici lineárních soustav, čímž určíme vývoj os.
  • Nelineární soustava určuje středovou trajektorii.
  • Každá z trojice lineárních soustav určuje vývoj sféry počátečních podmínek (což představuje trojici ortonormálních vektorů).
• Stanovíme přírůstky všech tří os a provedeme reortonormalizaci vektorů os.
• K ortonormalizaci použijeme Gramm-Schmittův postup.
• Vypočteme lokální Ljapunovovy exponenty.
• Lokální Ljapunovův exponent pro jednu osu v čase t vypočteme ze vzorce:
  
  kde t je dosažený čas a p(t) je přírůstek vektoru osy v čase t.

Ljapunovovo spektrum získáme jako limitu posloupnosti lokálních Ljapunovových exponentů.

Vlastní výsledky

Postup výpočtu Ljapunovova spektra, který byl výše uveden, jsem použil na systému, jenž simuluje chování nelineárního konzolového nosníku, zatíženého harmonickým zatížením. Pro stanovení Ljapunovových exponentů jsem vybral systém s parametry, při nichž se systém chová chaoticky (alespoň jeden Ljapunovův exponent je kladný, viz obrázek 1) a to zejména proto, že stanovení Ljapunovova spektra pro chaotický systém je numericky nejnáročnější.

Vývoj lokálního Ljapunovova exponentu, který odpovídá ose stavové proměnné j pro nulové počáteční podmínky, je vidět na obrázku 2. Na obrázku 3 je vývoj Ljapunovova exponentu odpovídajícího ose stavové proměnné w, taktéž pro nulové počáteční podmínky. Hodnota lokálního Ljapunovova exponentu odpovídající ose stavové proměnné q je předem známá a výpočet tuto hodnotu potvrzuje.

Nejprve jsem ověřil, zda jsou vývoje Ljapunovových exponentů závislé na volbě množství cyklů pro ortonormalizaci vektorů os. Zjistil jsem pro rozsah 10 až 1 000 cyklů pro krok h = 0.0001s, že jsou vývoje nezávislé (viz obrázek 4).

Pro stanovení Ljapunovova spektra bylo potřeba provést výpočty pro různé počáteční podmínky. Odhad globálních Ljapunovových exponentů vyšel značně rozdílný i pro poměrně dlouhé časové období (ve svých výpočtech jsem sledoval časové období od 0 do 150 sekund při kroku h = 0.0001s), viz tab. 1. Další komplikací při odhadování globálních Ljapunovových exponentů je, že závislost není taková, aby se dala snadno aproximovat funkcí s asymptotickým chováním. V průběhu Ljapunovových exponentů jsou totiž globální oscilace, jak je vidět na obrázcích 2 a 3. Proto byl odhad proveden prostým aritmetickým průměrem z poslední jedné čtvrtiny řešení (čas 112 až 150 sekund).

Obr. 1: Projekce podivného atraktoru

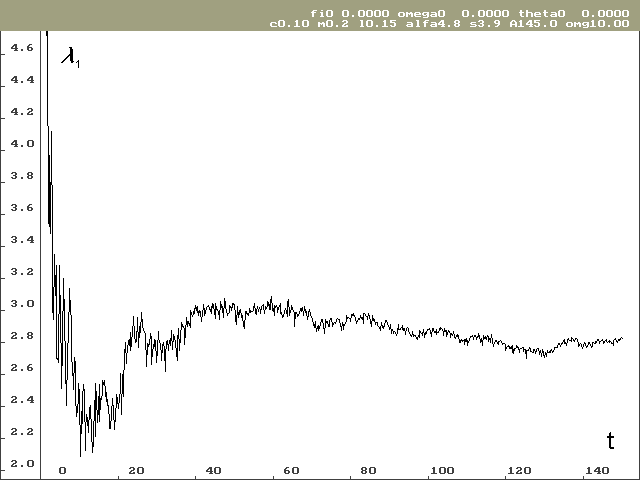
Obr. 2: Závislost Ljapunovova exponentu l ₁ na čase pro nulové počáteční podmínky. Odhadovaná hodnota je 2.79 bit.s^-1.

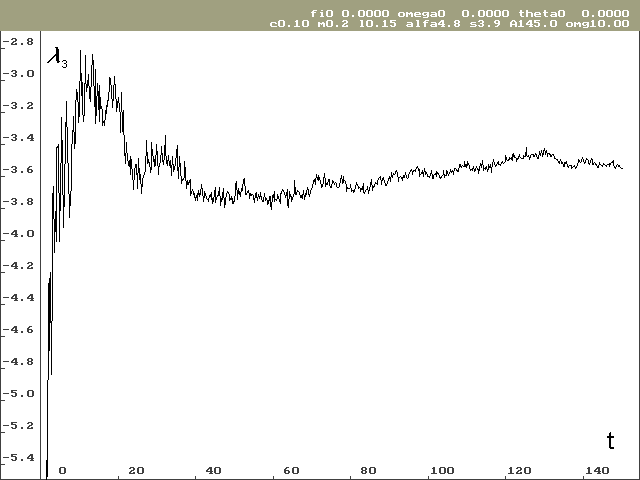
Obr. 3: Závislost Ljapunovova exponentu l ₃ na čase pro nulové počáteční podmínky. Odhadovaná hodnota je -3.51 bit.s^-1.

Obr. 4: Porovnání vlivu počtu cyklů na průběh Ljapunovova exponentu l ₁.

Pro statistické vyhodnocení, tedy zjištění odhadu Ljapunovova spektra a odhadu chyb, jsem provedl výpočet Ljapunovova spektra pro různé počáteční podmínky. Průběh závislosti lokálního Ljapunovova exponentu, pro dané počáteční podmínky, lze vidět po kliknutí na hodnotu odhadu Ljapunovova exponentu v tabulce. Výsledné odhady, které jsou uvedeny v tabulce č. 2, jsou aritmetickým průměrem ze všech odhadů pro jednotlivé počáteční podmínky a pravděpodobná chyba odhadu byla zjištěna ze vzorce:

kde

je směrodatná odchylka.

počáteční podmínky			spektrum Ljapunovových exponentů
j(0)	w(0)	q(0)	l 1	l 2	l 3
0	0	0	2.79	0.00	-3.51
0.05	0	0	2.97	0.00	-3.69
0	0.1	0	2.89	0.00	-3.61
0.05	0.1	0	2.71	0.00	-3.43
0	0	1	2.58	0.00	-3.30
0.05	0	1	2.67	0.00	-3.39
0	0.1	1	2.66	0.00	-3.38
0.05	0.1	1	2.81	0.00	-3.53

Výpočet	spektrum Ljapunovových exponentů
	l 1	l 2	l 3
statistický	2.76 ± 0.03	0.00	-3.48 ± 0.03

Závěr

Z uvedeného vyplývá:

• Ve velkém rozsahu počtu cyklů pro ortonormalizaci je průběh lokálních Ljapunovových exponentů pro studovaný systém nezávislý na počtu cyklů (u Lorenzova či Roeslerova systému tomu tak není).
• Průběh lokálních Ljapunovových exponentů, pro studovaný systém, nelze aproximovat funkcemi s asymptotickým chováním pro získání odhadů globálních Ljapunovových exponentů.
• Dobrý odhad Ljapunovova spektra lze získat aritmetickým průměrem odhadů spektra pro různé počáteční podmínky.

Příloha

Ljapunovovo spektrum	typ atraktoru	obrázek
(-,-,-)	pevný bod
(0,-,-)	limitní cyklus
(0,0,-)	dvoj-torus
(+,0,-)	podivný atraktor