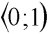, jako realizace náhodné veličiny R s rovnoměrným rozdělením (tj. s rozdělením, jehož rozdělovací funkce je konstantní). Potom například, chceme-li vygenerovat hod kostkou jako číslo y, lze psát:
Abstract
The solved problem is compiling of special generator of random numbers for application in cryptographic algorithm. There is used theory of chaos. Approximate distribution function is used for transformation of generated numbers. Approximation is realized by means of the least square method.
Úvod
Při vytváření vlastního šifrovacího programu jsem zjistil, že pro bezpečnost řešení bude vhodné, vytvořím-li si vlastní generátor náhodných čísel. Vzhledem k tomu, že výsledky chaotických procesů jsou nepředvídatelné, pokusil jsem se takový proces využít k vytvoření generátoru.
V případě, že pomineme jevy kvantové fyziky (neurčitost chodu elektronického stroje), potom ve stejném počítači probíhá proces dle programu vždy naprosto stejně, má-li stejné počáteční podmínky. Často také víme, jak počáteční podmínky ovlivní výsledek procesu. V mnoha případech si však přejeme, aby proces, dle daných počátečních podmínek, byl nepředvídatelný (pod pojmem nepředvídatelný myslíme fakt, že pokud proces s danými počátečními podmínkami nespustíme, nevíme k jakému výsledku dospěje). Příkladem může být simulace hodu kostkou, karetní hra, kdy počítač vytváří sestavy karet, nebo vytvoření umělého pohoří. Algoritmicky řečeno výběr z více možností, pro které požadujeme, aby se realizovaly s určitou danou pravděpodobností.
Generování náhodných čísel v počítači je nejjednodušší způsob jak zajistit, aby nějaký proces probíhal odlišně či nepředvídatelně. Volíme proto nějakou počáteční podmínku, např. systémový čas, kterou použijeme jako vstup do generátoru náhodného procesu v rámci programu.
Výstupem z generátoru je pak nejlépe číslo r z intervalu 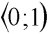, jako realizace náhodné veličiny R s rovnoměrným rozdělením (tj. s rozdělením, jehož rozdělovací funkce je konstantní). Potom například, chceme-li vygenerovat hod kostkou jako číslo y, lze psát:
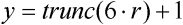
kde funkce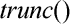 
odstraní desetinnou část argumentu.
Rovnice generátoru
Rovnice generátoru je funkce F, zobrazující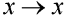 
, která se poprvé aplikovala v biologii na vývoj populací živočichů [1]:
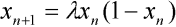
kde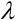 
je růstový faktor z intervalu 
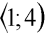a xn je hodnota populace po n-tém kroku iteračního procesu pro počáteční hodnotu x0 z intervalu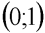 
Rozdělení
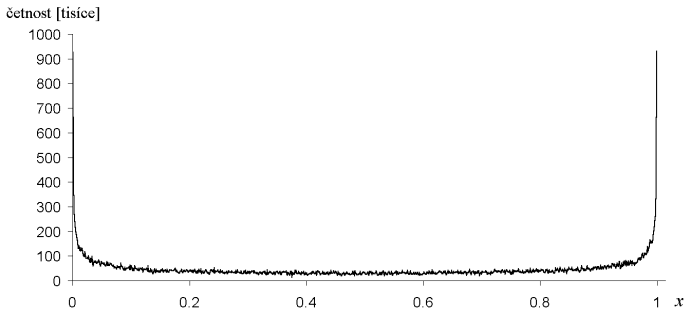
Pro zvolené 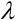= 4 - 1.024.10-12 a po provedení 47 miliónů realizací dostáváme histogram absolutních četností na obr. 1.
Závěr
Čísla generovaná tímto algoritmem nemají rovnoměrné rozdělení, které je nejvhodnější pro obecný generátor. Lze je však snadno vybírat a transformovat na rovnoměrné rozdělení, například pomocí aproximace distribuční funkce metodou nejmenších čtverců. Tento postup byl úspěně řešen a bylo dosaženo relativně dobré přesnosti.
Poděkování
Práce na tomto příspěvku byla podporována z prostředků projektu GA ČR 103/00/0603 a výzkumného záměru CEZ: J22/98: 261100007.
Literatura
[1] James Gleick, Chaos: vznik nové vědy, Ando Publishing, Brno, 1996